chapter6递归求解反射系数

Chapter 6

6.1.1 分层叠加

我们考虑由均匀半空间所包围的区域 $(z_A，z_C)$，$z_A$和$z_C$处的弹性参数具有连续性。然后通过在$z_A$和$z_C$之间的$z_B$层分割分层来划分该区域。我们设想在 zB 处引入一个无限小的均匀区域，链式规则与(5.38)一样

$$\mathbf{Q}(z_{A},z_{C})=\mathbf{Q}(z_{A},z_{B})\mathbf{Q}(z_{B},z_{C})\tag{6.1}$$

由于$z_A \le z_B \le z_C$，我们可以对(6.1)中的每个Q采用(5.45)表示法。(6.1) 的左侧由$Q(z_A, z_C)$的分区组成

$$\begin{aligned} &(\mathbf{T_D^{AC}})^{-1}=(\mathbf{T_D^{AB}})^{-1}[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}](\mathbf{T_D^{BC}})^{-1} \\ &\mathbf{R_D^{AC}(T_D^{AC})^{-1}=T_U^{AB}R_D^{BC}(T_D^{BC})^{-1}+R_D^{AB}(T_D^{AB})^{-1}[I-R_U^{AB}R_D^{BC}](T_D^{BC})^{-1}} \\ &(\mathbf{T_D^{AC}})^{-1}\mathbf{R_U^{AC}}=(\mathbf{T_D^{AB}})^{-1}\mathbf{R_U^{AB}}\mathbf{T_U^{BC}}+(\mathbf{T_D^{AB}})^{-1}[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}](\mathbf{T_D^{BC}})^{-1}\mathbf{R_U^{BC}} \end{aligned}\tag{6.2}$$

对于$Q(z_A, z_C)$的剩余部分有一个更复杂的表达式

借助$(T^{AC}_D)^{−1}$的表达式，我们可以恢复整体反射和透射矩阵。向下的矩阵是

$$\begin{aligned}\mathbf{T_D^{AC}}&=\mathbf{T_D^{BC}}[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]^{-1}\mathbf{T_D^{AB}},\\\mathbf{R_D^{AC}}&=\mathbf{R_D^{AB}}+\mathbf{T_U^{AB}}\mathbf{R_D^{BC}}[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]^{-1}\mathbf{T_D^{AB}}\end{aligned}\tag{6.3}$$

向上的矩阵也有类似的结构

$$\begin{aligned} &\mathbf{T}_{\mathrm{U}}^{\mathrm{AC}} =\mathbf{T_{U}^{AB}[I-R_{D}^{BC}R_{U}^{AB}]^{-1}T_{U}^{BC}} \\ &\mathbf{R}_{\mathrm{U}}^{\mathrm{AC}} =\mathbf{R_{U}^{BC}}+\mathbf{T_{D}^{BC}}\mathbf{R_{U}^{AB}}[\mathbf{I}-\mathbf{R_{D}^{BC}}\mathbf{R_{U}^{AB}}]^{-1}\mathbf{T_{U}^{BC}} \end{aligned}\tag{6.4}$$

6.1.2 加法规则的推广

在5.2节中，我们展示了反射和透射矩阵与基本应力-位移矩阵BVC的相互关系，其列对应于水平zC的上行和下行波。现在我们利用这个关系将加法规则推广到一般反射矩阵。

在$z_A$水平上我们可以构造$B_{VC}(z_A)$

$$\mathbf{B}_{\mathrm{VC}}(z_{{A}}) =\mathbf{P}(z_{{A}},z_{{C}})\mathbf{D}(z_{{C}}) =\mathbf{P}(z_{A},z_{B})\mathbf{P}(z_{B},z_{C})\mathbf{D}(z_{C})\tag{6.5}$$

采用传播链规则(2.89)。我们现在可以用$z_B$和$z_C$之间的波传播子Q来改写(6.5)，使用(5.47)

$$\mathbf{B}_{{VC}}(z_{{A}}) =\mathbf{P}(z_{A},z_{B})\mathbf{D}(z_{B})\mathbf{Q}(z_{B},z_{C}) =\mathbf{B}_\mathrm{VB}(z_\mathrm{A})\mathbf{Q}(z_\mathrm{B},z_\mathrm{C}), \tag{6.6}$$

我们认识到基本矩阵$B_{VB}$对应于$z_B$处的上下波。在分块形式中，我们看到两个基本矩阵通过出现在$Q(z_B, z_C)$中的区域$(z_B, z_C)$的反射和透射性质连接起来。与牵引力部分有相同的形式 即

$$\begin{aligned}{W}_{{UC}}(z_{{A}})&={W}_{{UB}}(z_{{A}})\mathbf{T}_{{U}}^{{BC}}-\{{W}_{{DB}}(z_{{A}})+{W}_{{UB}}(z_{{A}})\mathbf{R}_{{D}}^{{BC}}\}(\mathbf{T}_{{D}}^{{BC}})^{-1}\mathbf{R}_{{U}}^{{BC}}\\{W}_{{DC}}(z_{{A}})&=\left({W}_{{DB}}(z_{{A}})+{W}_{{UB}}(z_{{A}})\mathbf{R}_{{DC}}^{{BC}}\right)(\mathbf{T}_{{D}}^{{BC}})^{-1}\end{aligned}\tag{6.7}$$

考虑在$z = z_A$处施加自由表面边界条件，根据$B_{VC}$的牵引部分, 由(5.63)式可得自由表面处$z_C$之间的向上反射矩阵为

$$\mathbf{R_{U}^{fC}}=-\mathbf{T_{DC}^{-1}}(z_{A})\mathbf{T_{UC}(z_{A})}\tag{6.8}$$

如果我们现在用$B_{VB}$和BC反射和透射矩阵来代替$B_{VC}$，我们就有了

$$\mathbf{R_{U}^{fC}=T_{D}^{BC}(T_{DB}(z_{A})+T_{UB}(z_{A})R_{D}^{BC})^{-1}T_{UB}(z_{A})T_{U}^{BC}+R_{U}^{BC}}\tag{6.9}$$

从(6.8)得到了

$$\mathbf{R}_{U}^{fC}=\mathbf{R}_{U}^{BC}+\mathbf{T}_D^{BC}\mathbf{R}_{U}^{fB}[\mathbf{I}-\mathbf{R}_D^{BC}\mathbf{R}_{U}^{fB}]^{-1}\mathbf{T}_{U}^{BC}\tag{6.10}$$

这个加法关系的形式与我们前面关于向上矩阵的关系(6.4)完全相同。在地震场的所有边界条件下，反射的加法关系的结构将是相同的，因此位移和牵引力的线性组合在某些深度上消失。对应反射矩阵的计算需要计算类似式(6.8)的表达式，其中T由位移和牵引的其他组合代替。由于相同的线性算子将应用于式(6.7)的两边，我们总是会从(6.10)中提取一个reverberation operator

当我们要求自由面牵引力消失时，我们进一步推广了传输的附加规则，因为表面位移$W^{fC}_U$可以表示为

$$\mathbf{W_{U}^{fC}}=\mathbf{W_{U}^{fB}}[\mathbf{I}-\mathbf{R_{D}^{BC}}\mathbf{R_{U}^{fB}}]^{-1}\mathbf{T_{U}^{BC}}\tag{6.11}$$

当我们使用(2.68)时，它与(6.4)的形式相同，用于向上传输。

如果我们把$z_B$置于自由曲面(z = 0)的正下方，就可以得到这个位移算子的一个特别有用的形式

$$\mathbf{W}_{\mathrm{U}}^{\mathrm{fC}}=\mathbf{W}_{\mathrm{F}}[\mathbf{I}-\mathbf{R}_{\mathrm{D}}^{\mathrm{0C}}\mathbf{R}_{\mathrm{F}}]^{-1}\mathbf{T}_{\mathrm{U}}^{\mathrm{0C}}\tag{6.12}$$

其中$W_F = m_{U0} + m_{D0}R_F$，用D ( 0 + )的分拆表示.这个位移算子在半空间对埋藏源激励的响应表达式中起着重要的作用，正如我们在7.3节中所见。

6.1.3 附加规则的解释

加法规则( 6.3 )，( 6.4 )使得我们可以构造一个区域' AC '的整体反射和透射矩阵，但是我们还没有对区域' AB '和' BC '的性质如何结合给出任何物理解释

作为说明，我们取向下的矩阵

$$\begin{aligned}&\mathbf{T_D^{AC}=T_D^{BC}[I-R_U^{AB}R_D^{BC}]^{-1}T_D^{AB}}\\&\mathbf{R_D^{AC}=R_D^{AB}+T_U^{AB}R_D^{BC}[I-R_U^{AB}R_D^{BC}]^{-1}T_D^{AB}}\end{aligned}\tag{6.13}$$

其中上、下区域的性质通过矩阵逆$[I-R^{AB}_UR^{BC}_D]^{-1}$的作用而耦合

对于SH波，$R^{AB}_U R^{BC}_D$只是反射系数的乘积

$$\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}=(\mathbf{R_U^{HH}})(\mathbf{R_D^{HH}})\tag{6.14}$$

为了简单起见，我们去掉上标AB，BC

对于P-SV波，矩阵乘积生成

$$\mathbf{R_D^{AB}}\mathbf{R_D^{BC}}=\begin{pmatrix}\mathbf{R_U^{PP}}\mathbf{R_D^{PP}}+\mathbf{R_U^{PS}}\mathbf{R_D^{SP}}&\mathbf{R_U^{PP}}\mathbf{R_D^{PS}}+\mathbf{R_U^{PS}}\mathbf{R_D^{SS}}\\\mathbf{R_U^{SP}}\mathbf{R_D^{PP}}+\mathbf{R_U^{SS}}\mathbf{R_D^{SP}}&\mathbf{R_U^{SP}}\mathbf{R_D^{PS}}+\mathbf{R_U^{SS}}\mathbf{R_U^{SS}}\end{pmatrix}\tag{6.15}$$

并且每个部分代表了物理上可行的反射元素的组合

当我们根据行列式和矩阵共轭直接计算逆$[I-R^{AB}_UR^{BC}_D]^{-1}$时，我们在所有耦合波情况下都遇到了困难。例如，在P - SV波行列式的展开中，我们产生了反射组合

$$\mathrm{R_U^{SP}R_D^{PS}R_U^{PS}R_D^{SP},\quad R_U^{PP}R_D^{PP}R_U^{SS}R_D^{SS}}\tag{6.16}$$

由于波形的切换，任何物理过程都无法实现(Cisternas, Betancourt & Leiva, 1973)。如果我们对矩阵的逆作级数展开式，这个困难就可以解决了

$$[I-R_{{U}}^{AB}R_{{D}}^{BC}]^{-1}=I+R_{{U}}^{AB}R_{{D}}^{BC}+R_{{U}}^{AB}R_{{D}}^{BC}R_{{U}}^{AB}R_{{D}}^{BC}+...\tag{6.17}$$

其中，所有相互作用的组合在物理上都是可行的。随着这个逆的展开，向下的反射和透射矩阵具有了表示形式

$$\begin{aligned} &R_{D}^{AC} =\mathbf{R_D^{AB}}+\mathbf{T_U^{AB}}\mathbf{R_D^{BC}}\mathbf{T_D^{AB}}+\mathbf{T_U^{AB}}\mathbf{R_D^{BC}}\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}\mathbf{T_D^{AB}}+..., \\ &T_{D}^{AC} =\mathbf{T_D^{BC}}\mathbf{T_D^{AB}}+\mathbf{T_D^{BC}}\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}\mathbf{T_D^{AB}}+... \end{aligned}\tag{6.18}$$

而这些序列中更高的项包含了$R_{AB}^U R_{BC}^D$的更高次幂

序列(6.18)的示意图如下图示，其中我们设想了在zA处入射向下的行波，从而产生反射和透射项。通过从右到左的阅读，可以找到(6.17)中每个术语的物理内容。

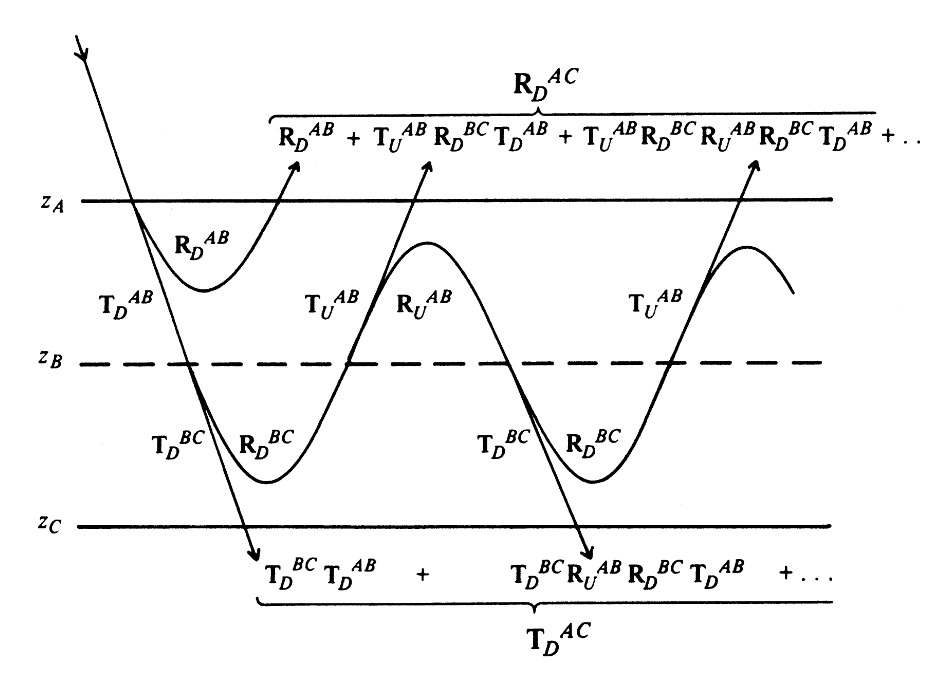
由图可以清晰的看到每一项的计算过程, 序列中高阶项的项包括' AB '区和' BC '区之间进一步的内部相互作用。总响应式( 6.3 )包含了所有这些内部混响，因此我们将$[I-R^{AB}_UR^{BC}_D]^{-1}$作为区域'AC'的混响算子。

在透射序列(6.18)中也可以看到类似的模式。第一项$T^{BC}_D T^{AB}_D$对应的是通过整个区域的直接传播。高阶项包括由$R^{AB}_U R^{BC}_D$的幂表示的连续内部混响

通过对混响算符的这种解释，我们看到，如果我们截断$[ I-R^{AB}_U R^{BC}_D]$^{-1}到M + 1项的展开式，我们将在$R^{AC}_D$，T^{AC}_D的近似式( 6.18 )中包含M个内部混响。如果这些反射和透射量本身被用于加法规则的进一步应用中，则可能的内部混响是累积的，并且最大可以出现nM个这样的腿，其中n是RAC D或TAC D出现在响应完全扩展中的次数。

Kennett (1975,1979a)和Stephen(1977)使用截断展开来研究多次反射，并限制对地震波场部分的关注。对于复倍数的研究，使用近似来抑制一个区域内的所有内部混响是特别方便的

$$^0\mathbf{R}_D^{A{C}}=\mathbf{R}_D^{A{B}}+\mathbf{T}_U^{A{B}}{R}_D^{B{C}}\mathbf{T}_D^{A{B}}\tag{6.19}$$

只允许一个内部混响

$$^{1}\mathbf{R}_D^{AC}=\mathbf{R}_D^{AB}+\mathbf{T}_{U}^{AB}\mathbf{R}_D^{BC}[\mathbf{I}+\mathbf{R}_{U}^{AB}\mathbf{R}_D^{BC}]\mathbf{T}_D^{AB}\tag{6.20}$$

并且当全混响序列包含矩阵逆时

$$\mathbf{R_D^{AC}}=\mathbf{R_D^{AB}}+\mathbf{T_U^{AB}}\mathbf{R_D^{BC}}[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]^{-1}\mathbf{T_D^{AB}}\tag{6.21}$$

同样的项组合出现在(6.20)，(6.21)中，对于P-SV波，我们只需要计算2 × 2矩阵逆。因此，当需要在'AC'中进行多个内部交互时，计算完整响应(6.21)更方便、更有效。

在上面的讨论中，我们考虑了从“AB”和“BC”区域反射时P波和SV波之间转换的可能性。如果这种反射可以忽略不计，混响算符本质上就是P波和SV波的单独算符

$$[\mathbf{I}-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]^{-1}\approx\begin{bmatrix}[1-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]_{\mathbf{PP}}^{-1}&0\\0&[1-\mathbf{R_U^{AB}}\mathbf{R_D^{BC}}]_{\mathbf{SS}}^{-1}\end{bmatrix}\tag{6.22}$$

如果转换可能只发生在'AB'区域，情况会更加复杂，因为现在P和SV内部倍数之间存在部分耦合。每一种波型的混响序列都将被该波型的转换倍数所产生的贡献所改变:$\mathrm{R_U^{PS}}\mathrm{R_D^{SS}}\mathrm{R_U^{PS}}\mathrm{R_D^{PP}}.$

6.2 堆叠层的反射

在任何均匀层中没有反射，意味着一个均匀矩阵堆栈的反射矩阵在很大程度上取决于界面系数。通过层的传输给出了调制界面效应的相位项。对于一个均匀层堆栈，在前一节中引入的加法规则可以用于构造两阶段递归过程中的反射和传输矩阵。通过一层的相位延迟和界面项交替引入。

6.2.1 递归方案

考虑z1 < z < z2中的一个均匀层覆盖在z2 < z < z3中的一堆这样的层上。我们假设z2−处的反射和透射矩阵是已知的，并写为:

$$\mathbf{R}_\mathrm{D}(z_2-)=\mathbf{R}_\mathrm{D}(z_2-,z_3+)\tag{6.23}$$

然后，我们可以使用加法规则和(5.49)加入对应于通过均匀层的透射的相位项，以计算z1+处界面下方的反射和透射矩阵。因此

$$\begin{aligned}\mathbf{R}_\mathrm{D}(z_1+)&=\mathbf{E}_\mathrm{D}^{12}\mathbf{R}_\mathrm{D}(z_2-)\mathbf{E}_\mathrm{D}^{12}\\\mathbf{T}_\mathrm{D}(z_1+)&=\mathbf{T}_\mathrm{D}(z_2-)\mathbf{E}_\mathrm{D}^{12}\\\mathbf{T}_\mathrm{U}(z_1+)&=\mathbf{E}_\mathrm{D}^{12}\mathbf{T}_\mathrm{U}(z_2-)\end{aligned}\tag{6.24}$$

其中$E^{12}_D$为向下通过层传播的相位收入(3.45)。加法规则的进一步应用允许我们包含界面z1的反射和透射矩阵，例如:

$$\mathbf{R}_D^1=\mathbf{R}_D(z_1-,z_1+)\tag{6.25}$$

z1界面上方的向下反射和透射矩阵取决于界面项和先前计算的向下量

$$\begin{aligned}\mathbf{R}_\mathrm{D}(z_1-)&=\mathbf{R}_\mathrm{D}^1+\mathbf{T}_\mathrm{U}^1\mathbf{R}_\mathrm{D}(z_1+)[1-\mathbf{R}_\mathrm{U}^1\mathbf{R}_\mathrm{D}(z_1+)]^{-1}\mathbf{T}_\mathrm{D}^1,\\\mathbf{T}_\mathrm{D}(z_1-)&=\mathbf{T}_\mathrm{D}(z_1+)[1-\mathbf{R}_\mathrm{U}^1\mathbf{R}_\mathrm{D}(z_1+)]^{-1}\mathbf{T}_\mathrm{D}^1,\end{aligned}\tag{6.26}$$

向上的矩阵采用不那么简单的形式，因为我们实际上是在波传播系统最复杂的层面上增加了一层

$$\begin{aligned}\mathbf{R}_\mathbf{U}(z_1-)&=\mathbf{R}_\mathbf{U}(z_2-)+\mathbf{T}_\mathbf{D}(z_1+)\mathbf{R}_\mathbf{U}^1[1-\mathbf{R}_\mathbf{D}(z_1+)\mathbf{R}_\mathbf{U}^1]^{-1}\mathbf{T}_\mathbf{U}(z_1+)\\\mathbf{T}_\mathbf{U}(z_1-)&=\mathbf{T}_\mathbf{U}^1[1-\mathbf{R}_\mathbf{D}(z_1+)\mathbf{R}_\mathbf{U}^1]^{-1}\mathbf{T}_\mathbf{U}(z_1+)\end{aligned}\tag{6.27}$$

如果需要，截断混响序列可以代替矩阵逆，以给出有限的近似结果。

加法规则的这两种应用可以递归地计算全反射矩阵和透射矩阵。我们从z3的分层基础开始，计算界面矩阵，例如$R^3_D$，它也将是$R_D(z3−)$。我们使用(6.24)将堆叠反射和透射矩阵步进到stack中最低层的顶部, 然后我们使用(6.26)-(6.27)的接口加法关系将stack矩阵带到该接口的上端。(6.24)和(6.26)-(6.27)的循环允许我们对任意数量的层进行一次一层的stack操作。

对于向下的矩阵$R_D，T_D$ ( 6.24 )，( 6.26 )在计算过程中只需要保持向下的stack矩阵。当需要向上的矩阵时，通常更方便地从分层的顶部开始分别计算它们，并每次向下工作一层。所得到的构造方案具有与( 6.24 )，( 6.26 )类似的结构，并且很容易通过从自由表面系数开始而不是界面系数来适应自由表面反射矩阵

在固定的慢度p下，所有的界面矩阵$R^i_D，T^i_D$等都是频率无关的, 因此每一层中频率依赖项通过相位引入$E^{12}_D$, 如果存储界面系数，则可以在一个慢度p的多个频率下快速执行计算。

当波在任何层中消失时，我们选择的垂直慢度$q_\alpha, q_\beta$意味着$E^{12}_D$需满足

$$\exp\{\operatorname{i}_{\alpha}(z_2-z_1)\}=\exp\{-\omega|{q}_{\alpha}|(z_2-z_1)\}\tag{6.28}$$

当$q^2_\alpha \le z_1$, 我们总是让$z_2 > z_1$所以不会出现随频率增长的指数项。这意味着即使在高频率下，递归格式在数值上也是稳定的。