chapter5反射与透射

P81 chapter 5 反射与透射

在两个半空间中嵌入一平面$Z=Z_I$,

$$\mathbf{b}(z_\text{I}-)=\mathbf{D}_-(z_\text{I}-)\mathbf{v}_-(z_\text{I})\tag{5.1}$$

$$\mathbf{b}(z_\text{I}+)=\mathbf{D}_+(z_\text{I}+)\mathbf{v}_+(z_\text{I})\tag{5.2}$$

此处的应力-位移向量b应具有连续性$b(z_I-)=b(z_I+)$, 故

$$\mathbf{v}_{-}(\boldsymbol{z}_{\mathrm{I}}-) =\mathbf{D}_{-}^{-1}(z_\text{I}{ - })\mathbf{D}_{+}(z_\textbf{I}{ + })\mathbf{v}_{+}(z_\text{I}{ + }) =\mathbf{Q}(z_\text{I}-,z_\textbf{I}+)\mathbf{v}_+(z_\text{I}+)$$

对于SH波，结合(3.16), (3.24)可得

$$\begin{bmatrix}\mathrm{H}_{\mathrm{U}-}\\\mathrm{H}_{\mathrm{D}-}\end{bmatrix}=\frac{\epsilon_{\beta-}\epsilon_{\beta+}}{\beta_{-}\beta_{+}}\begin{bmatrix}\mu_{-}\mathrm{q}_{\beta-}&\mathrm{i}\\\mu_{-}\mathrm{q}_{\beta-}&-\mathrm{i}\end{bmatrix}\begin{bmatrix}1\\-\mathrm{i}\mu_{+}\mathrm{q}_{\beta+}\mathrm{~i}\mu_{+}\mathrm{q}_{\beta+}\end{bmatrix}\begin{bmatrix}\mathrm{H}_{\mathrm{U}+}\\\mathrm{H}_{\mathrm{D}+}\end{bmatrix}\tag{5.6}$$

标准化$\epsilon_{\beta-}/\beta_-=(2\mu_-q_{\beta-})^{1/2}$上式可化为

$$\begin{bmatrix}\mathrm{H}_{\mathrm{U}-}\\\mathrm{H}_{\mathrm{D}-}\end{bmatrix}=\frac1{2(\mu_{-}\mu_{+}q_{\beta-}q_{\beta+})^{1/2}}\begin{bmatrix}\mu_{-}q_{\beta-}+\mu_{+}q_{\beta+}\mu_{-}q_{\beta-}-\mu_{+}q_{\beta+}\\\mu_{-}q_{\beta-}-\mu_{+}q_{\beta+}\mu_{-}q_{\beta-}+\mu_{+}q_{\beta+}\end{bmatrix}\begin{bmatrix}\mathrm{H}_{\mathrm{U}+}\\\mathrm{H}_{\mathrm{D}+}\end{bmatrix}\tag{5.7}$$

矩阵Q中的所有元素都依赖于乘积$\mu q_\beta$, 其在斜向传播的SH波起到阻抗的作用

对于P-SV耦合波,结合(3.17)

$$\mathbf{Q}(z_\mathbf{I}-,z_\mathbf{I}+)=\mathbf{D}_-^{-1}(z_\mathbf{I}-)\mathbf{D}_+(z_\mathbf{I}+)\tag{5.15}$$

(5.2)化为

$$\begin{bmatrix}v_{\mathrm{U}-}\\v_{\mathrm{D}-}\end{bmatrix}=\begin{bmatrix}\mathrm{Q}_{\mathrm{U}\mathrm{U}}&\mathrm{Q}_{\mathrm{U}\mathrm{D}}\\\mathrm{Q}_{\mathrm{D}\mathrm{U}}&\mathrm{Q}_{\mathrm{D}\mathrm{D}}\end{bmatrix}\begin{bmatrix}v_{\mathrm{U}+}\\v_{\mathrm{D}+}\end{bmatrix}\tag{5.16}$$

通过(5.15)得到Q的形式

$$\mathbf{Q}(z_\text{I}{ - },z_\text{I}{ + }) =\mathrm{i}\begin{bmatrix}-\mathbf{n}_{\mathrm{D-}}^\mathrm{T}&\mathbf{m}_{\mathrm{D-}}^\mathrm{T}\\\mathbf{n}_{\mathrm{U-}}^\mathrm{T}&-\mathbf{m}_{\mathrm{U-}}^\mathrm{T}\end{bmatrix} \begin{bmatrix}\mathbf{m}_{\mathrm{U+}}&\mathbf{m}_{\mathrm{D+}}\\\mathbf{n}_{\mathrm{U+}}&\mathbf{n}_{\mathrm{D+}}\end{bmatrix} =\mathrm{i}\begin{bmatrix}\mathbf{m}_{D-}^{\mathrm{T}}\mathbf{n}_{\mathrm{U}+}-\mathbf{n}_{D-}^{\mathrm{T}}\mathbf{m}_{\mathrm{U}+}&\mathbf{m}_{\mathrm{D}-}^{\mathrm{T}}\mathbf{n}_{\mathrm{D}+}-\mathbf{n}_{\mathrm{D}-}^{\mathrm{T}}\mathbf{m}_{\mathrm{D}+}\\\mathbf{n}_{\mathrm{U}-}^{\mathrm{T}}\mathbf{m}_{\mathrm{U}+}-\mathbf{m}_{\mathrm{U}-}^{\mathrm{T}}\mathbf{n}_{\mathrm{U}+}&\mathbf{n}_{\mathrm{U}-}^{\mathrm{T}}\mathbf{m}_{\mathrm{D}+}-\mathbf{m}_{\mathrm{U}-}^{\mathrm{T}}\mathbf{n}_{\mathrm{D}+}\end{bmatrix}\tag{5.17}$$

(5.17)可以被认为具有(2.68)中矩阵传播不变量的形式

连接界面两侧的上行和下行波分量的关系式(5.16)因此可以写成

$$\begin{bmatrix}v_{\mathrm{U-}}\\v_{\mathrm{D-}}\end{bmatrix}=\mathrm{i}\begin{bmatrix}<\mathbf{m_{D-}},\mathbf{m_{\mathrm{U+}}}>&-<\mathbf{m_{\mathrm{U-}}},\mathbf{m_{\mathrm{U+}}}>\\<\mathbf{m_{\mathrm{D-}}},\mathbf{m_{\mathrm{D+}}}>&-<\mathbf{m_{\mathrm{U-}}},\mathbf{m_{\mathrm{D+}}}>\end{bmatrix}\begin{bmatrix}v_{\mathrm{U+}}\\v_{\mathrm{D+}}\end{bmatrix}\tag{5.18}$$

虽然我们已经在P - SV波传播的背景下引入了( 5.18 )，但这种形式是相当一般的，如果我们使用mU，nU等的SH波形式，( 3.100 )，我们将恢复( 5.7 )。对于完全各向异性传播，我们将使用3 × 3矩阵mU，mD。

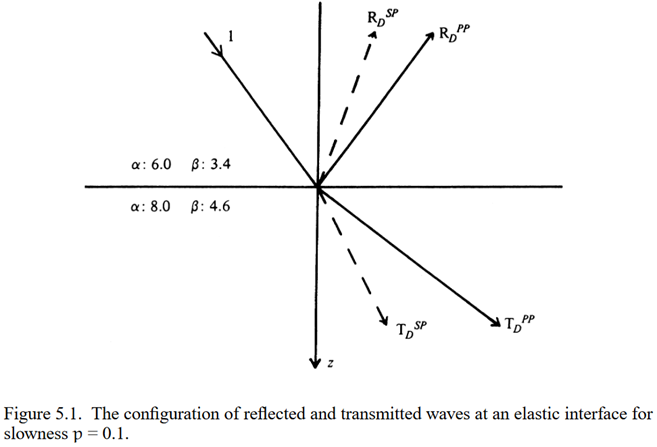
考虑一个包含P波和SV波的下行波系统，介质为' - '。当它与界面相互作用时，在介质' - '中得到反射P波和SV波，在介质' + '中得到透射下行波(图5.1 )。在介质' + '中不会产生上行行波，因此vU + = 0。我们现在定义一个向下入射的反射矩阵RI D，它的元素是反射系数

$$v_{\mathrm{U}-}=\mathbf{R}_{\mathrm{D}}^{\mathrm{I}}v_{\mathrm{D}-}\quad\mathrm{i.e.}\quad\begin{bmatrix}\mathbf{P}_{\mathrm{U}-}\\\mathbf{S}_{\mathrm{U}-}\end{bmatrix}=\begin{bmatrix}\mathbf{R}_{\mathrm{D}}^{\mathrm{PP}}\mathbf{R}_{\mathrm{D}}^{\mathrm{PS}}\\\mathbf{R}_{\mathrm{D}}^{\mathrm{SP}}\mathbf{R}_{\mathrm{D}}^{\mathrm{SS}}\end{bmatrix}\begin{bmatrix}\mathbf{P}_{\mathrm{D}-}\\\mathbf{S}_{\mathrm{D}-}\end{bmatrix}\tag{5.19}$$

将介质' - '中的上行波和下行波元素联系起来。同样连接通过界面的下行波分量通过传输矩阵

$$v_{\mathrm{D}+}=\mathrm{T}_{\mathrm{D}}^{\mathrm{I}}v_{\mathrm{D}-}\quad\mathrm{i.e.}\quad\begin{bmatrix}\mathrm{P}_{\mathrm{D}+}\\\mathrm{S}_{\mathrm{D}+}\end{bmatrix}=\begin{bmatrix}\mathrm{T}_{\mathrm{D}}^{\mathrm{PP}}\mathrm{T}_{\mathrm{D}}^{\mathrm{PS}}\\\mathrm{T}_{\mathrm{D}}^{\mathrm{SP}}\mathrm{T}_{\mathrm{D}}^{\mathrm{SS}}\end{bmatrix}\begin{bmatrix}\mathrm{P}_{\mathrm{D}-}\\\mathrm{S}_{\mathrm{D}-}\end{bmatrix}\tag{5.20}$$

我们选择了转换系数$R^{PS}_D$等的约定，使反射矩阵和透射矩阵的索引遵循标准矩阵模式，这对操作非常有用。

对于这些入射的下行波，波要素是相关联的

$$\begin{bmatrix}v_{{U}-}\\v_{{D}-}\end{bmatrix}=\begin{bmatrix}{Q}_{{U}{U}}&{Q}_{{U}{D}}\\{Q}_{{D}{U}}&{Q}_{{D}{D}}\end{bmatrix}\begin{bmatrix}0\\v_{{D}+}\end{bmatrix}\tag{5.21}$$

因此，反射和传输矩阵可以根据Q的划分来找到

$$\mathbf{T_D^I=(Q_{DD})^{-1}},\quad\mathbf{R_D^I=Q_{UD}(Q_{DD})^{-1}}\tag{5.22}$$

(5.11)为SH波。利用Q ( 5.17 )，( 5.18 )分拆的显式形式，我们有

$$\begin{aligned}&{T_D^I=i<m_{U-},m_{D+}>^{-1},}\\&{R_D^I=-<m_{D-},m_{D+}><m_{U-},m_{D+}>^{-1}}\end{aligned}\tag{5.23}$$

尖括号括号符号作为一个相异算子，mD-和mD+之间的不匹配决定了反射矩阵$R^I_D$。

介质“+”中的入射入射波系统将在介质“+”中产生反射波，在介质“-”中产生透射波。在介质' - '中不会产生下行波，因此vD - = 0，现在我们有

$$\begin{bmatrix}v_{\mathrm{U}-}\\0\end{bmatrix}=\begin{bmatrix}\mathrm{Q}_{\mathrm{U}\mathrm{U}}&\mathrm{Q}_{\mathrm{U}\mathrm{D}}\\\mathrm{Q}_{\mathrm{D}\mathrm{U}}&\mathrm{Q}_{\mathrm{D}\mathrm{D}}\end{bmatrix}\begin{bmatrix}v_{\mathrm{U}+}\\v_{\mathrm{D}+}\end{bmatrix}\tag{5.24}$$

我们定义这些向上入射波的反射和透射矩阵为

$$v_{\mathrm{D}+}=\mathbf{R}_{\mathrm{U}}^\mathrm{I}v_{\mathrm{U}+},\quad v_{\mathrm{U}-}=\mathbf{T}_{\mathrm{U}}^\mathrm{I}v_{\mathrm{U}+}\tag{5.25}$$

并且从(5.24)可以由Q的分量构造$R^I_U，T^I_U$

$$\begin{aligned}&\mathbf{R_{{U}}^I=-(Q_{DD})^{-1}Q_{DU,}}\\&\mathbf{T_{{U}}^I=Q_{{U}{U}}-Q_{{U}{D}}(Q_{{D}{D}})^{-1}Q_{{D}{U}}}\end{aligned}\tag{5.26}$$

对于这个单一界面，我们当然可以通过交换$R^I_D, T^I_D$表达式中的+和-来得到相同的结果;但是，正如我们将看到的，目前的方法可以很容易地扩展到更复杂的情况。根据Q ( 5.21 )，( 5.26 )分划的反射和透射矩阵的表达式，我们可以将界面矩阵重构为

$$\mathbf{Q}(z_\text{I}{ - },z_\text{I}{ + }) =\mathbf{D}_-^{-1}(z_\text{I}{ - })\mathbf{D}_+(z_\text{I}{ + }) \left.=\left[\begin{array}{cc}\mathbf{T_{U}^{I}-R_{D}^{I}(T_{D}^{I})^{-1}R_{U}^{I}}&\mathbf{R_{D}^{I}(T_{D}^{I})^{-1}}\\-\mathbf{(T_{D}^{I})^{-1}R_{U}^{I}}&(\mathbf{T_{D}^{I}})^{-1}\end{array}\right.\right]\tag{5.28}$$

特征向量矩阵仅依赖于慢度p，因此Q与频率无关。所有的界面系数都具有这一性质

向上的反射和传输矩阵可以用界面处的传播不变量来表示为

$$\begin{aligned} &R_{u}^{\mathrm{I}} =-\mathrm{<{m}_{{U}-},{m}_{{D}+}>^{-1}}\mathrm{<{m}_{{U}-},{m}_{{U}+}>} \\ &{T_u^I} =-\mathrm{i<m_{D+},m_{U-}>^{-1}=(T_{D}^{I})^{T}} \end{aligned}\tag{5.29}$$

我们现在可以利用位移和应力变换矩阵mU，nU等的表达式( 3.37 )来构造PSV波情况下的反射和透射矩阵。所有的界面系数矩阵都依赖于$<\mathfrak{m}_{{U}-},\mathfrak{m}_{{D}+}>^{-1}$，因此$\text{det}<\mathfrak{m}_{{U}-},\mathfrak{m}_{{D}+}>$将出现在每个反射和透射系数的分母中。透射系数是Q的各个元素除以这个行列式，而反射系数则是Q的二阶次元素的比值形式。行列式计算如下

$$\begin{array}{ll} \mathrm{det<}\mathbf{m}_{\text{U}-},\mathbf{m}_{\text{D}+}>=& \epsilon_{\alpha-}\epsilon_{\alpha+}\epsilon_{\beta-}\epsilon_{\beta+} \{[2p^2\Delta\mu(q_{\alpha-}-q_{\alpha+})+(p_{-}q_{\alpha+}+p_{+}q_{\alpha-})] \times[2p^2\Delta\mu({q}_{\beta-}-{q}_{\beta+})+({p}_{-}{q}_{\beta+}+{p}_{+}{q}_{\beta-})] \\ &+p^2[2\Delta\mu(q_{\alpha-}q_{\beta+}+p^2)-\Delta\rho][2\Delta\mu(q_{\beta-}q_{\alpha+}+p^2)-\Delta\rho]\} \end{array}\tag{5.30}$$

引入了界面剪切模量和密度的对比度$\Delta \mu = \mu_- - \mu_+, \Delta \rho = \rho_--\rho_+$ Stoneley(1924)指出，如果这个行列式消失，我们就有可能在远离界面的自由界面波衰减到两侧介质中。这些Stoneley波有一个相当有限的存在范围，因为对于大多数合理的密度差，剪切速度β -和β +必须几乎相等，才能使(5.30)为零。Stoneley波的慢度始终大于$[\min(\beta_-, \beta_+)]^{-1}$

上述推导的反射矩阵和透射矩阵的表达式也可以直接利用传播不变量推导出来P87 (5.31)-(5.34)

重要公式

对于P-SV波

传播不变量

$$<m_U,m_D>=({m}_{{U}}^\mathrm{T}{n}_{{D}}-{n}_{{U}}^\mathrm{T}{m}_{{D}})=iI\tag{3.39}$$

$$\begin{aligned} &R_{u}^{{I}} =-<{m}_{{U}-},{m}_{{D}+}>^{-1}<{m}_{{U}-},{m}_{{U}+}> \\ &{T_u^I} =-{i<m_{D+},m_{U-}>^{-1}=(T_{D}^{I})^{T}} \end{aligned}\tag{5.29}$$

$$\mathbf{T}_{\mathrm{D}}^{{I}}=\mathrm{i<m}_{\mathrm{U}-},{m}_{\mathrm{D}+}>^{-1}\tag{5.34}$$

反射系数随慢度的变化

我们选择将系数表示为慢度的函数，而不是传统的入射角，因为我们可以使用P波和S波的共同参考，从而更清楚地显示许多特征

分层区

将zA和zC处的应力-位移矢量通过传播算子连接

$$\mathbf{b}(z_{{A}})=\mathbf{P}(z_{{A}},z_{{C}})\mathbf{b}(z_{{C}})\tag{5.35}$$

在这两个均匀的半空间中，我们将应力-位移场分解为上下的P波和S波，利用b向量的连续性

$$\begin{aligned}\mathbf{b}(z_{{A}})&=\mathbf{D}(z_{{A}})\mathbf{v}(z_{{A}}-)\\\mathbf{b}(z_{{C}})&=\mathbf{D}(z_{{C}})\mathbf{v}(z_{{C}}+)\end{aligned}\tag{5.36}$$

由于弹性性质在$z_A, z_c$处具有连续性，因此上下均匀半空间中的波矢v之间的关系为

$$\mathbf{v}(z_{А}-)=\mathbf{D}^{-1}(z_{А})\mathbf{P}(z_{А},z_\text{С})\mathbf{D}(z_{С})\mathbf{v}(z_{С}+)\tag{5.37}$$

结合(5.35)和(5.36)时。传播矩阵$Q(z_A, z_C)$为

$$\mathbf{v}(z_{А}-)=\mathbf{Q}(z_{А},z_{С})\mathbf{v}(z_{С}+)\tag{5.38}$$

根据传播矩阵的链式法则

$$\begin{aligned} \mathbf{Q}(z_{A},z_{C})& =\mathbf{D}^{-{1}}(z_{{A}})\mathbf{P}(z_{{A}},z_{{B}})\mathbf{P}(z_{{B}},z_{{C}})\mathbf{D}(z_{{C}}), \\ &=\mathbf{D}^{-1}(z_{{A}})\mathbf{P}(z_{{A}},z_{{B}})\mathbf{D}(z_{{B}})\mathbf{D}^{-1}(z_{{B}})\mathbf{P}(z_{{B}},z_{{C}})\mathbf{D}(z_{{C}}) \end{aligned}\tag{5.39}$$

也就是

$$\mathbf{Q}(z_{{A}},z_{\mathsf{C}})=\mathbf{Q}(z_{{A}},z_{\mathsf{B}})\mathbf{Q}(z_{{B}},z_{{C}})\tag{5.40}$$

其逆可以表达为

$$\mathbf{Q}(z_{A},z_{C})=\mathbf{Q}^{-1}(z_{C},z_{A})$$

我们将均匀半空间中的波矢分为上波和下波部分，并对$Q(z_A, z_C)$进行剖分，使得(5.38)变为与(5.16)一样的结构

$$\begin{bmatrix}v_\mathrm{U}(z_\mathrm{A}-)\\v_\mathrm{D}(z_\mathrm{A}-)\end{bmatrix}=\begin{bmatrix}\mathrm{Q}_\mathrm{UU}&\mathrm{Q}_\mathrm{UD}\\\mathrm{Q}_\mathrm{DU}&\mathrm{Q}_\mathrm{DD}\end{bmatrix}\begin{bmatrix}v_\mathrm{U}(z_\mathrm{C}+)\\v_\mathrm{D}(z_\mathrm{C}+)\end{bmatrix}\tag{5.42}$$

对于从半空间z < zA入射的下行波，反射和透射矩阵类似(5.22)计算给出

$$\begin{aligned}\mathbf{T_D^{AC}}&=\mathbf{T_D}(z_{A},z_{C})=(\mathbf{Q_{DD}})^{-1}\\\mathbf{R_D^{AC}}&=\mathbf{R_D}(z_{A},z_{C})=\mathbf{Q_{UD}}(\mathbf{Q_{DD}})^{-1}\end{aligned}\tag{5.43}$$

当入射上行波在z > zC时，传输和反射矩阵由下式给出

$$\begin{aligned}& \mathbf{T_{U}^{AC}=Q_{UU}-Q_{UD}(Q_{DD})^{-1}Q_{DU}}\\&\mathbf{R_{U}^{AC}=-(Q_{DD})^{-1}Q_{DU}}\end{aligned}\tag{5.44}$$

对于单个界面，在固定慢度p下，$Q(z_I- , z_I+)$与频率无关(5.28)，但对于分层区域$Q(z_A, z_C)$包含频率依赖的传播项$P(z_A, z_C)$，因此$T^{AC}_D,R^{AC}_D$等与频率$\omega$有关。

结合(5.43)，(5.44)得到$Q(z_A, z_C)$的形式, 通过在向上和向下入射波的反射和透射矩阵分块的方法类似(5.28)

$$\mathbf{Q}(z_{{A}},z_{{C}})=\begin{bmatrix}\mathbf{T}_{{U}}^{{A}{C}}-\mathbf{R}_{{D}}^{{A}{C}}(\mathbf{T}_{{D}}^{{A}{C}})^{-1}\mathbf{R}_{\mathsf{U}}^{{A}{C}}&\mathbf{R}_{{D}}^{{A}{C}}(\mathbf{T}_{{D}}^{{A}{C}})^{-1}\\-(\mathbf{T}_{{D}}^{{A}{C}})^{-1}\mathbf{R}_{{U}}^{{\lambda}{C}}&(\mathbf{T}_{{D}}^{{A}{C}})^{-1}\end{bmatrix}\tag{5.45}$$

从下层往上看,也就是(5.45)的逆, 当分层区域反转时，向上的反射和透射矩阵实际上是向下的矩阵

$$\mathbf{Q}(z_\mathbf{C},z_\mathbf{A})=\begin{bmatrix}(\mathbf{T}_\mathbf{U}^{\mathbf{A}\mathbf{C}})^{-1}&-(\mathbf{T}_\mathbf{U}^{\mathbf{A}\mathbf{C}})^{-1}\mathbf{R}_\mathbf{D}^{\mathbf{A}\mathbf{C}}\\\mathbf{R}_\mathbf{U}^{\mathbf{A}\mathbf{C}}(\mathbf{T}_\mathbf{U}^{\mathbf{A}\mathbf{C}})^{-1}&\mathbf{T}_\mathrm{D}^{\mathbf{A}\mathbf{C}}-\mathbf{R}_\mathrm{U}^{\mathbf{A}\mathbf{C}}(\mathbf{T}_\mathrm{U}^{\mathbf{A}\mathbf{C}})^{-1}\mathbf{R}_\mathrm{D}^{\mathbf{A}\mathbf{C}}\end{bmatrix}\tag{5.46}$$

当我们希望根据(zE, zF)的反射和透射性质来表示波传播子Q( zE , zF)时，如果zE≥zF，我们使用( 5.45 )的形式，但是如果zE小于zF，我们将使用(5.46)的形式。

应力-位移传播子P(zA, zC)可以由波传播子Q(zA, zC)还原为

$$\mathbf{P}(z_{{A}},z_{{C}})=\mathbf{D}(z_{{A}})\mathbf{Q}(z_{{A}},z_{\mathsf{C}})\mathbf{D}^{-1}(z_{{C}})\tag{5.47}$$

这个关系使我们对传播子的物理本质有了一定的认识。$D^{-1}(z_C)$的作用是将$z_C$处的应力和位移场分解为其上、下两部分。在$z_A$处对应的上行波和下行波是由波传播者Q的作用产生的，而波传播者Q需要通过分层了解两个方向的传播特性。特征向量矩阵$D(z_A)$然后从波分量中重建$z_A$处的位移和牵引力。

波传播子的一个特别简单的情况是在均匀介质时

$$\mathbf{Q}_{\mathfrak{un}}(z_{{A}},z_{\mathsf{C}}) =\exp\{\mathrm{i}\omega(z_{A}-z_{C}){\Lambda}\} =\begin{bmatrix}\mathbf{E_D^{AC}}&\mathbf{0}\\\mathbf{0}&(\mathbf{E_D^{AC}})^{-1}\end{bmatrix}\tag{5.48}$$

其中$E_D^{AC}$为$z_A\to z_C$相位收入矩阵(phase income matrix)

由于$Q_{un}$的非对角线划分为空，因此$R^{AC}_D,R^{AC}_U$均为零，如预期。透射矩阵为

$$\mathbf{T}_{\mathrm{D}}^{\mathrm{AC}}=\mathbf{E}_{\mathrm{D}}^{\mathrm{AC}}\quad\mathbf{T}_{\mathrm{U}}^{\mathrm{AC}}=\mathbf{E}_{\mathrm{D}}^{\mathrm{AC}}\tag{5.49}$$

5.2.2 位移矩阵表示

我们现在引入一个基本的应力-位移矩阵$B_V$，它的列是分层中某一层上行波和下行波对应的b向量。我们将对$B_V$的位移和牵引矩阵分区特别感兴趣，并将使用这些来概括反射和传输矩阵的概念。

在分层内的$z=z_G$平面上，我们构造了单位振幅P波和S波在具有$z_G$弹性特性的均匀介质中产生的位移

$$W_{UG}=m_{UG}\tag{5.50}$$

其中$m_{UG}$为特征向量矩阵$D(z_G)$的位移部分, 牵引力部分为

$$T_{UG}=n_{UG}\tag{5.51}$$

构造单位振幅下行的P波和S波的位移矩阵和牵引矩阵

$$W_{\mathrm{DG}}={m}_{\mathrm{DG}},\quad{T}_{\mathrm{DG}}={n}_{\mathrm{DG}}\tag{5.52}$$

实际上，我们在zG处引入了一个无穷小的均匀区域，在这个区域中，我们可以定义上行和下行波，就像推导波传播器的链式法则一样。从(5.50)-(5.52)中介绍的位移和牵引矩阵，我们构造了一个基本的应力-位移矩阵

$$\mathbf{B}_\mathrm{VG}=\begin{bmatrix}\mathbf{W}_\mathrm{UG}&\mathbf{W}_\mathrm{DG}\\\mathbf{T}_\mathrm{UG}&\mathbf{T}_\mathrm{DG}\end{bmatrix}\tag{5.53}$$

在zG处，这个矩阵简化为$D(z_G)$。在远离$z_G$的水平上，我们可以利用$D(z_G)$当作参考平面按照分层介质的传播矩阵来构造$B_{VG}$

$$\mathbf{B}_\mathrm{VG}(z_\mathrm{J})=\mathbf{P}(z_\mathrm{J},z_\mathrm{G})\mathbf{D}(z_\mathrm{G})\tag{5.54}$$

按照(5.47)替换掉$P(z_J,zG)$得到

$$\mathbf{B}_\mathrm{VG}(z_\mathrm{J})=\mathbf{D}(z_\mathrm{J})\mathbf{Q}(z_\mathrm{J},z_\mathrm{G})\tag{5.55}$$

如果$z_J$位于$z_G$的上方，我们由分块表示构造$B_{VG}(z_J)$，(5.45)为波传播子，(3.36)通过$m_{DJ}, m_{UJ}$为特征向量矩阵$D(z_J)$。位移矩阵$W_{UG}, W_{DG}$由$(z_J, z_G)$的反射和透射矩阵给出

$$\begin{aligned} &W_{\mathrm{UG}}(z_{\mathrm{J}}) =\mathbf{m_{UJ}}\mathbf{T_{U}^{JG}}-(\mathbf{m_{DJ}}+\mathbf{m_{UJ}}\mathbf{R_{D}^{JG}})(\mathbf{T_{D}^{JG}})^{-1}\mathbf{R_{U}^{JG}} \\ &W_{\mathrm{DG}}(z_{\mathrm{J}}) =(\mathbf{m}_{\mathrm{DJ}}+\mathbf{m}_{\mathrm{UJ}}\mathbf{R}_{\mathrm{D}}^{\mathrm{JG}})(\mathbf{T}_{\mathrm{D}}^{\mathrm{JG}})^{-1} \end{aligned}\tag{5.56}$$

牵引矩阵$T_{UG}，T_{DG}$同理

(5.56)可得到

$${W}_\mathrm{UG}(z_\mathrm{J})+{W}_\mathrm{DG}(z_\mathrm{J})\mathbf{R}_\mathrm{U}^\mathrm{JG}=\mathbf{m}_\mathrm{UJ}\mathbf{T}_\mathrm{U}^\mathrm{JG}\tag{5.57}$$

方程左边的场可以理解为向上的波入射在$(z_G , z_J)$区域上,且$z_J$只由透射的波组成

如果$z_J$位于$z_G$下方，我们用(5.38)??作为波的传播子，此时位移矩阵$W_{UG}，W_{DG}$由下式给出

$$\begin{aligned} &W_{\mathrm{UG}}(z_{\mathrm{J}}) =(\mathbf{m_{UJ}}+\mathbf{m_{DJ}}\mathbf{R_{U}^{GJ}})(\mathbf{T_{U}^{GJ}})^{-1} \\ &W_{\mathrm{DG}}(z_{\mathrm{J}}) =\mathbf{m}_\mathrm{DJ}\mathbf{T}_\mathrm{D}^\mathrm{GJ}-(\mathbf{m}_\mathrm{UJ}+\mathbf{m}_\mathrm{DJ}\mathbf{R}_\mathrm{U}^\mathrm{GJ})(\mathbf{T}_\mathrm{U}^\mathrm{GJ})^{-1}\mathbf{R}_\mathrm{D}^\mathrm{GJ} \\ \end{aligned}\tag{5.58}$$

可得

$$\boldsymbol{W_\mathrm{DG}}(z_\mathrm{J})+\boldsymbol{W_\mathrm{UG}}(z_\mathrm{J})\mathbf{R_\mathrm{D}^\mathrm{GJ}}=\boldsymbol{m_\mathrm{DJ}}\mathbf{T_\mathrm{D}^\mathrm{GJ}}\tag{5.59}$$

对应于$(z_G, z_J)$区域上的一个入射下行波系统

对于位移场$W_{UG}, W_{DG}$，矩阵$<W_{UG}, W_{DG}>$与深度无关，可以方便地在$z_G$本身求值

$$<\mathbf{W}_{\mathrm{UG}},\mathbf{W}_{\mathrm{DG}}>=<\mathbf{m}_{\mathrm{UG}},\mathbf{m}_{\mathrm{DG}}>=\mathrm{iI}\tag{5.60}$$

通过上述已经可得，位移矩阵$W_{UG}，W_{DG}$与分层的反射和透射性质密切相关。事实上，如果我们可以构造两个不同起始点$z_A$和$z_C$的基本矩阵$B_{VA}, B_{VC}$，就可以得到$(z_A, z_C)$区的反射和透射矩阵。

考虑$z_A$处的入射下行波，在区域$z_A\le z \le z_C$上，这将引起由$R^{AC}_D$的反射。由此产生的位移场可表示为

$$\mathbf{W}_{\mathbf{R}}(z)=\mathbf{W}_{\mathbf{DA}}(z)+\mathbf{W}_{\mathbf{UA}}(z)\mathbf{R}_{\mathbf{D}}^{\mathbf{AC}}\tag{5.61}$$

从(5.59)中我们可以看到，在$z_C$处，这个位移场具有$m_{DC}T^{AC}_D$的形式，与牵引力部分的形式相似。我们使用$W_{DC}(z)$是位移$m_{DC}$和牵引力$n_{DC}$在$z_C$处产生的位移场，因此我们有$W_R(z)$的另一种表示。

$$W_{{R}}(z)=W_{{D}{C}}T_{{D}}^{{A}{C}}\tag{5.62}$$

在$(z_A, z_C)$的任何层上，我们必须能够将这些基于$z_A$和$z_C$的的位移和牵引表示等同起来,即

$$\begin{gathered} \boldsymbol{W}_{\mathrm{DA}}(z)+\boldsymbol{W}_{\mathrm{UA}}(z)\boldsymbol{R}_{\mathrm{D}}^{\boldsymbol{AC}}=\boldsymbol{W}_{\mathrm{DC}}(z)\mathbf{T}_{\mathrm{D}}^{\boldsymbol{AC}} \\ \mathbf{T}_{\mathrm{DA}}(z)+\mathbf{T}_{\mathrm{UA}}(z)\mathbf{R}_{\mathrm{D}}^{{AC}}=\mathbf{T}_{\mathrm{DC}}(z)\mathbf{T}_{\mathrm{D}}^{{AC}} \end{gathered}\tag{5.63}$$

这些方程的一个特例出现在界面问题(5.31) - (5.32)中，我们的求解方法与之类似。我们利用2.2节中矩阵不变量的性质求解$R_D^{AC}, T_D^{AC}$

得到性质:向下的反射矩阵是对称的

$$R_D^{AC}=(R_D^{AC})^T$$

对于zC处的上行波入射场,我们有包含向上反射和传输矩阵的位移和牵引方程

$$\begin{aligned}{W}_{{UC}}(z)+{W}_{{DC}}\mathbf{R}_{{U}}^{{AC}}&={W}_{{UA}}(z)\mathbf{T}_{{U}}^{\mathsf{AC}},\\{T}_{{UC}}(z)+{T}_{{DC}}\mathbf{R}_{{U}}^{{AC}}&={T}_{{UA}}(z)\mathbf{T}_{{U}}^{{AC}}.\end{aligned}\tag{5.72}$$

如果我们可以构造出分层区域( zA , zC)内的位移和牵引力，对应于均匀半空间中向上和向下行波在zA和zC处产生的位移和牵引力，我们就可以形成该区域的所有反射和透射矩阵。我们推导出的反射和透射性质的表达式不依赖于任何关于( zA , zC)内参数分布性质的假设。因此，对于任意的衰减区域，我们建立了对称关系

$$\mathbf{R_D^{AC}}=(\mathbf{R_D^{AC}})^{\mathsf{T}},\quad\mathbf{R_U^{AC}}=(\mathbf{R_U^{AC}})^{\mathsf{T}},\quad\mathbf{T_U^{AC}}=(\mathbf{T_D^{AC}})^{\mathsf{T}}\tag{5.75}$$

5.3.3 反射矩阵一般化

借助位移场WUG，WDG，我们可以扩展反射矩阵的概念，以适应地震波场上的一般线性边界条件

作为例子，我们考虑z = 0处牵引力消失的自由面条件。我们构造了WUG，WDG的线性叠加

$$\boldsymbol{W_{1G}}(z)=\boldsymbol{W_{\mathrm{UG}}}(z)+\boldsymbol{W_{\mathrm{DG}}}(z)\mathbf{R_{U}^{fG}}\tag{5.76}$$

并选择自由面反射矩阵$R^{fG}_U$，使其在z = 0处相关联的牵引力为零，即

$${T}_{1{G}}(0)={T}_{{U}{G}}(0)+{T}_{{D}{G}}(0)\mathbf{R}_{{U}}^{\mathrm{fG}}=0\tag{5.77}$$

因此我们有一个对称的反射矩阵

$$\mathbf{R_{U}^{fG}=-[T_{DG}(0)]^{-1}T_{UG}(0)}\tag{5.78}$$

牵引矩阵也可以表示为从表面到$z_G$的传播算子与$z_G$处的特征向量矩阵的乘积的一部分$z_G:[P(0, z_G)D(z_G)]$。我们可以把$W_{1G}(z)$看成是由于从具有$z_G$性质的均匀半空间入射到$z_G$处的波系所产生的位移场。一个有用的相关量是入射上行波引起的表面位移矩阵$W_{1G}(0)$????，记为$W^{fG}_U$

该矩阵共享透射矩阵的部分属性，表示为

$$\mathbf{W}_{{U}}^{\mathrm{fG}}=-\mathrm{i}[{T}_{\mathrm{DG}}(0)]^{-{T}}\tag{5.79}$$

这可以通过消除地表位移和牵引力方程之间的$R^{fG}_U$得到

如果我们将水平zG移动到表面正下方，即$z_G = 0+$，则得到自由表面的反射矩阵

$$\mathbf{R_{F}}=\mathbf{R_{U}^{f0}}=-\mathbf{n_{D0}^{-1}}\mathbf{n_{U0}}\tag{5.80}$$

在固定的慢度下该矩阵频率无关的。

对于SH波，由(3.38)可得

$$\mathbf{R_{F}^{HH}}=1$$

而对于P-SV波，由(3.37)

$$\begin{bmatrix}{R}_\mathrm{F}^\mathrm{PP}{R}_\mathrm{F}^\mathrm{SP}\\{R}_\mathrm{F}^\mathrm{SP}{R}_\mathrm{F}^{SS}\end{bmatrix}=\frac1{4{p}^2{q}_{\alpha0}{q}_{\beta0}+{v}^2} \begin{bmatrix}4{p}^2{q}_{\alpha0}{q}_{\beta0}-{v}^2&\mathrm{4ip}{\upsilon}({q}_{\alpha0}{q}_{\beta0})^{1/2}\\4\mathrm{ip}\mathfrak{\upsilon}({q}_{\alpha0}{q}_{\beta0})^{1/2}&\mathrm{4}{p}^2{q}_{\alpha0}{q}_{\beta0}-{v}^2\end{bmatrix}\tag{5.82}$$

其中

$$v=(2p^2-\beta_0^{-2})\tag{5.83}$$

通过我们的归一化，$R_F$是一个对称矩阵，得到

$${R}_{{F}}^{\mathrm{PP}}={R}_{{F}}^{\mathrm{SS}}\tag{5.84}$$

这些表面系数在慢度$p_R$处奇异，使得分母消失??即

$$(2p_{{R}}^2-\beta_0^{-2})^2+4p_{{R}}^2q_{\alpha0}q_{\beta0}=0\tag{5.85}$$

在自由表面处，由入射上行波引起的位移矩阵为

$$\mathbf{W_F}=(\mathbf{m_{UO}}+\mathbf{m_{D0}}\mathbf{R_F})\tag{5.86}$$

对于SH波，我们有一个简单的标量乘法

$$\mathrm{W_F^{HH}}=2\tag{5.87}$$

对于P-SV波，矩阵$W_F$具有更复杂的形式

$$\mathbf{W}_{\mathbf{F}}=\begin{bmatrix}-\mathrm{i}{q}_{\alpha0}\epsilon_{\alpha0}C_{1}&{p}\epsilon_{\beta0}C_{2}\\{p}\epsilon_{\alpha0}C_{2}&-\mathrm{i}{q}_{\beta0}\epsilon_{\beta0}C_{1}\end{bmatrix}\tag{5.88}$$

其中，由于存在从无限介质位移到自由表面位移的转换因子，$m_{U0}$的元素要更改

$$\begin{aligned} &\text{C1} =2\beta_0^{-2}(2p^2-\beta_0^{-2})/\{4p^2q_{\alpha0}q_{\beta0}+v^2\} \\ &\text{C2} =4\beta_0^{-2}{q}_{\alpha0}{q}_{\beta0}/\{4{p}^2{q}_{\alpha0}{q}_{\beta0}+{v}^2\} \end{aligned}\tag{5.89}$$

这些转换因子适用于传播波和倏逝波

为了在分层的基础上满足边界条件，例如，我们将构造一个位移场

$$\mathbf{W}_{2\mathrm{G}}(z)=\mathbf{W}_{\mathrm{DG}}(z)+\mathbf{W}_{\mathrm{UG}}(z)\mathbf{R}_{\mathrm{D}}^{\mathrm{GL}}\tag{5.90}$$

其中选择合适的$R^{GL}_D$，使得位移和牵引力的特定线性组合在某一深度处消失。如果分层在一个均匀的半空间下方$z > z_L$时，我们用通常的方法选择$R^{GL}_D$，使得在这个区域内没有上行波；此时的边界条件为

$$\mathbf{m}_{\mathrm{DL}}^{\mathrm{T}}\mathbf{T}_{2\mathrm{G}}(z_{\mathrm{L}})-\mathbf{n}_{\mathrm{DL}}^{\mathrm{T}}\mathbf{W}_{2\mathrm{G}}(z_{\mathrm{L}})=<\mathbf{W}_{\mathrm{DL}},\mathbf{W}_{2\mathrm{G}}>=0\tag{5.91}$$

对于在$z_L$以下随深度稳定增加的波速度分布，我们现在选择$R^{GL}_D$，使得当$z\to \infty$时，$W_2$趋于零。

5.2.4 球面分层的反射矩阵