Review

Entropy Regularized Nonlinear Joint PP-PS AVO Inversion Using Zoeppritz Equations

基于Zoeppritz方程的熵正则化非线性联合Pp - PS Avo反演

摘要

基于多分量地震数据的地震反演可以提高流体识别和岩性解释的精度。但对于剧烈的层间参数变化准确度差。

信息熵描述了系统的混沌性。将其作为先验约束，驱动反演参数的混沌性接近于先验测井数据的混沌性，可以提高反演结果的分辨率和稳定性。

为解决信息熵的高度非线性与Zoeppritz方程所带来的复杂，使用了QA算法，不仅可以缓解求解的复杂性，而且可以快速收敛到全局最优解

引言

精确Zoeppritz方程的非线性叠前AVO反演不需要考虑弱反射界面、小角度入射等约束条件，具有更广阔的发展空间

理论

熵正则化模型

将信息熵约束作为先验信息引入到AVO反演中，使反演参数的无序程度接近于实际数据的混沌程度，可以降低反演的不确定性，提高反演结果的精度。

信息熵定义为

$$H=-\sum^n_{i=1}p_i\log p_i$$

PS波对密度和横波速度更为敏感。因此，PP - PS波联合反演有利于更好地估计速度和密度，优化函数建立如下

$$E=\min_m\frac{1}{2}||d_{pp}-G_{pp}(m)||^2_2+\frac{\alpha}{2}||d_{ps}-G_{ps}(m)||^2_2+\beta||H_{inv}-H_{ref}||^2_2$$

$$H_{inv}=-\sum^n_{i=1}\frac{m_i}{Q}\ln\frac{m_i}{Q}$$

其中$Q=\sum^n_{i=1}|m_i|$， $\alpha=\frac{\sigma_{pp}}{\sigma_{ps}}$，$H_{inv}$表示待反演弹性参数的信息熵，$H_{ref}$表示参考信息熵，参考信息熵一般可以从测井资料中获得。

量子退火算法

量子退火( QA )是模拟退火( SA )的扩展和改进。

模拟退火

参考：模拟退火算法超详细教程，优化算法——模拟退火算法

算法思想来源于固体退火原理，是一种基于概率的算法。先从一个较高的初始温度出发，逐渐降低温度，直到温度降低到满足热平衡条件为止。在每个温度下，进行n轮搜索，每轮搜索时对旧解添加随机扰动生成新解，并按一定规则接受新解。

在任一温度时，对初始解添加随机扰动产生新解，若新解的目标函数值优于旧解，则接受新解；若新解差于旧解，则按一定概率接受旧解，从而有一定概率跳出局部最优解，找到全局最优解。

模拟退火算法描述：

若J( Y(i+1) )>= J( Y(i) ) (即移动后得到更优解)，则总是接受该移动

若J( Y(i+1) )< J( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

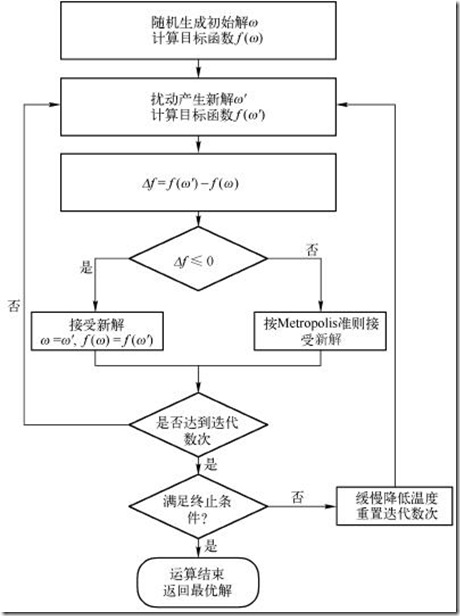
模拟退火算法的优点在于：不管函数形式多复杂，模拟退火算法更有可能找到全局最优解。

量子退火

量子退火算法

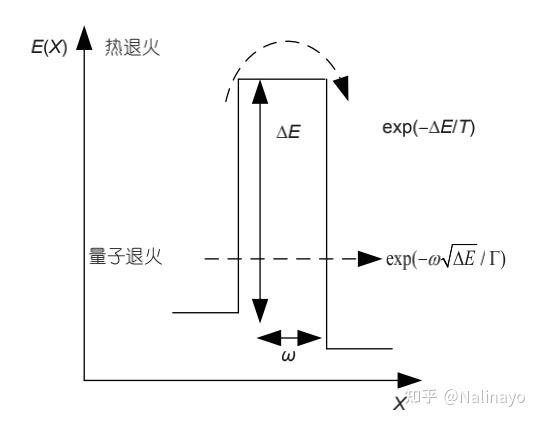
在经典的热退火情况下，系统要达到全局最小值，必须克服$O(N)$的较大势垒$\Delta E$为系统的大小（温度为$T$时，逃逸概率为$exp(-\Delta E /T)$），而在量子退火的情况下，系统可以隧穿势垒。如果势垒较窄，隧穿概率为$exp(- \omega \sqrt{\Delta E}/ \Gamma)$，其中$\Gamma$为隧穿波动场，$\omega$为势垒宽度。

曼哈顿函数为

$$H(t) = H_{pot} (t) + H_{kin}(t)$$

其表示量子退火算法中的评价函数（Cost Function），$H_{pot}(t)$表示势能，对应模拟退火算法的评价函数，$H_{kin}(t)$表示动能，在动能中加入量子波动（初始值较大，然后按照一定的进度表慢慢减小到零）。通常

$$H_{kin}(t)=-\Gamma(t)\sum^n_{i=1}\sigma^x_i$$

在地震反演中可用常数C代替$sigma^x_i$，曼哈顿函数表示为

$$H(t) = \Delta E +C\Gamma(t)$$

根据Metropolis - Hastings准则，接受概率可以写为

$$p=\left\{\begin{aligned} 1 \quad \Delta E\le0&\\ exp(- {\Delta E+C\Gamma(t)}/ \Gamma(t)) \quad \Delta E\gt 0& \end{aligned}\right.$$

衰减函数为

$$\Gamma(t)=\Gamma_0*exp(-1*\alpha*(iter-1)^\frac{1}{2})$$

其中$\Gamma_0$为初始值，$\alpha$为衰减因子

实验

在不同信噪比下对比了Tikhonov, PP波熵正则化，PP-PS联合熵正则化模拟退火算法，PP-PS联合熵正则化量子退火算法所得反演结果与相对误差，结果证明本文方法具有更高的准确度与抗噪性。

通过计算不同算法和不同信噪比下的反演结果与测井曲线之间的Pearson相关系数定量评估每种算法的反演性能

可观察到本文的方法具有较高的相关系数与较低的均方误差。

证明了QA比SA有较高的收敛速度

证明了引入信息熵约束得到更高的稳定性（通过计算相对误差的方差得到），同时发现信噪比对稳定性几乎没有影响