chapter7求解地震记录

7.3 响应在空间和时间上的恢复

我们刚刚看到了如何在变换域中构造一个分层半空间对埋藏源或地表源的激励的响应，作为频率ω和慢度p的函数。为了得到实际的地震图，我们仍然必须进行反变换. 对于地震图的P - SV波部分，我们有矢量调和展开( 2.55 )。

$$u_p(r,\phi,0,t)=\frac1{2\pi}\int_{-\infty}^\infty d\omega\mathrm{~e^{-i\omega t}\int_0^\infty dk~k\sum_m[UR_k^m+VS_k^m]}\tag{7.68}$$

通过引入张量场，我们可以用慢度p和表面位移向量w0来重铸这个积分

$$\mathbf{T_m}(\omega\text{pr})=[\mathbf{R_k^m},\mathbf{S_k^m}]^\mathsf{T}\tag{7.69}$$

因此，( 7.68 )可表示为

$$\mathbf{u_P(r,\phi,0,t)}=\frac1{2\pi}\int_{-\infty}^\infty d\omega\mathrm{e^{-i\omega t}}\omega^2\int_0^\infty dp\mathrm{~p\sum_mw_0^T(p,m,\omega)}\mathbf{T}_m(\omega pr)\tag{7.70}$$

对于SH响应$u_H$，我们有类似的形式

$$\mathbf{u}_H(r,\phi,0,t)=\frac1{2\pi}\int_{-\infty}^\infty\mathrm{d}\omega\operatorname{e^{-i\omega t}}\omega^2\int_0^\infty\mathrm{dp}\operatorname{p}\sum_{{m}}{W}_0^{T}({p},{m},\omega)\mathbf{T_m}(\omega\text{pr})\tag{7.71}$$

用谐波$T^m_k$来表示，我们把它重新写成一种形式来显示频率和慢度的关系。矢量谐波$R^m_k$, $S^m_k$和$T^m_k$(2.56)可以利用导数性质完全用贝塞尔函数项来表示

$${J}_{\mathfrak{m}}^{\prime}(x)={J}_{\mathfrak{m}-1}(x)-{m}{J}_{\mathfrak{m}}(x)/x\tag{7.72}$$

对于正交坐标向量$e_z, e_r, e_\phi$我们有谐波的显式形式。

$$\begin{aligned} \mathbf{R}_m(\omega pr)&={e_zJ_m(\omega pr)e^{im\phi}} \\\mathbf{S}_m(\omega pr)&=[{e_rJ_{m-1}(\omega pr)-(e_r-ie_\phi)mJ_m(\omega pr)/\omega pr]e^{im\phi}} \\\mathbf{T}_m(\omega pr)&=[-{e_\phi J_{m-1}(\omega pr)+(e_\phi+ie_r)mJ_m(\omega pr)/\omega pr]e^{im\phi}}\end{aligned}\tag{7.73}$$

这些形式在m≥0时最方便，但m < 0时的值很容易由下式得到

$$J_{-\mathfrak{m}}(x)=(-1)^{\mathfrak{m}}J_{\mathfrak{m}}(x)\tag{7.74}$$

只有在水平分量上，当|m| > 0时，我们才能得到依赖于$mJ_m(ωpr)/ωpr$的“近场”分量，它比沿坐标矢量方向的贡献衰减得更快。这些“近场”项将运动的径向分量和切向分量耦合在一起，因此在离震源较近的距离上，SV和SH运动的分量没有明显的分离。

当我们用一个由力和偶极子分量组成的等效点源来表示实际源时，方位角求和被限制在角度|m|<2范围内. 在对每个m进行频率和慢度积分后，这个和没有显著的复杂性。

对于二重积分(7.70)，我们必须选择进行频率积分和慢度积分的顺序。如果先计算慢度积分，则中间结果是特定位置的复频谱$\bar{\mathbf{u}}({r},\phi,{0},\omega)$。这种方法被称为谱方法，并已被用于通过对完全介质响应进行数值积分来计算理论地震记录的大多数尝试中(Kind, 1978;, 1980;Wang & Herrmann, 1980)。或者，当首先计算频率积分时，中间结果是每个慢度p的时间响应，对应于单个慢度分量对介质的照射。最后的结果是通过对慢度的积分得到的，这种方法称为慢度方法。虽然这种积分格式可以用于全响应，但迄今为止，大多数应用都是用于将响应分解为广义射线的近似方法，例如Cagniard方法, 以及Chapman提出的适用于平滑分层介质的方法.

谱方法

我们把第m个方位对地震记录的贡献谱作为慢度积分来构造

$$\bar{\mathbf{u}}({r},\mathfrak{m},0,\omega)=\omega^2\int_0^\infty\mathrm{dp~p}{w}_0^{{T}}({p},{m},\omega){T}_{{m}}(\omega{p}{r})\tag{7.75}$$

变换向量w0(p, m， ω)通过源跳变项S(zS)(4.62)依赖于方位阶m，并且每个阶引入不同的慢度依赖。当m为偶数时,w0(p, m， ω)是p的奇函数，当m为奇数时是p的偶函数。我们现在回想一下，$T_m(\omega pr)$的元素依赖于$J_m(\omega pr)e^{im\phi}$，因此我们可以将这种驻波形式分解成用汉克尔函数$H^{(1)}_m(\omega pr) H^{(2)}_m(\omega pr)$表示的行波形式。例如，$T^{(1)}_m(\omega pr)$表示从原点发出的波对应的谐波。

$$\begin{aligned} {J}_{{m}}({\omega pr})& =\frac12[{H}_{{m}}^{(1)}(\omega\text{pr})+{H}_{{m}}^{(2)}(\omega\text{pr})] \\ &=\frac12[{H}_{{m}}^{(1)}(\omega\text{pr})-\mathrm{e}^{\mathrm{im}\pi}{H}_{{m}}^{(1)}(-\omega\text{pr})] \end{aligned}\tag{7.76}$$

所以当我们使用w0的对称性时，我们可以将(7.75)表示为沿整个慢度轴的积分

$$\bar{\mathbf{u}}(r,m,0,\omega)=\frac12\omega|\omega|\int_{-\infty}^\infty dp\mathrm{~p}w_0^T(p,{m},\omega)T_{{m}}^{(1)}(\omega p\text{r})\tag{7.77}$$

其中p平面的积分轮廓在原点处的分支点上方取$H^{(1)}_m(\omega pr)$。这个形式清楚地表明，我们只对从源发散的波感兴趣。

对于较大的参数值，$H^{(1)}_m(ωpr)$可以用它的渐近形式代替

$${H}_{{m}}^{({1})}(\omega\text{pr})\sim(2/\pi\omega\text{pr})^{1/2}\mathsf{e}^{\{\mathrm{i}\omega\text{pr}-\mathrm{i}(2\text{m}+1)\pi/4\}}\tag{7.78}$$

在同样的近似下，矢量谐波具有沿正交坐标向量$ez, er, eφ$方向的场的特征。因此张量场$T^{(1)}_m(\omega pr)$近似为

$${T}_{{m}}^{(1)}\sim[\mathbf{e}_z,\mathbf{i}\mathbf{e}_r]^{{T}}(2/\pi\omega{p}{r})^{1/2}{e}^{\{\mathrm{i}\omega{p}{r}-\mathrm{i}(2{m}+1)\pi/4\}}\tag{7.79}$$

切谐波(SH波)

$${T_m^{(1)}(\omega pr)\sim-ie_\phi(2/\pi\omega pr)^{1/2}e^{\{i\omega pr-i(2m+1)\pi/4\}}}\tag{7.80}$$

在这个渐近极限中，对于位移的所有三个分量，我们在(7.77)的被积式中面临同样的慢度和距离依赖。

我们所描述的对称性质将被完全响应w0的近似所共享，因此我们将始终有可能使用驻波表达式(7.75)或行波表示(7.77)。

在慢速平面上，对于全表面响应w0，我们在p - sv情况下有分支点$p =±\alpha^{−1}_L$，在所有情况下$p =\pm \beta^{−1}_L$。对于p - sv和SH波的贡献，我们在$β^{-1}_L < p < \beta^{- 1}_{\min}$区域有一系列极点，其中$\beta_{\min}$是半空间中任何地方的最小剪切波速,通常在地面获得. 在SH波的慢度区间内，我们有更高模态的Love波极点，对于完全弹性介质来说，它位于实p轴上。对于P-SV波，我们有更高模态的瑞利极，其位置接近Love极，但不完全相同。此外，在半空间中，我们还得到了耦合消失的p波和SV波的基本瑞利模式;该模态的极限点为表面具有弹性的均匀半空间上的瑞利波慢度$p_{R0}$。极点的分布很大程度上取决于频率;在低频时，只有几个极点出现在$|p| > \beta^{−1}_L$ 中，而在高频时则有很多(见第11.3节)。

p - sv波情况下的奇异点集合如图7.3所示，ω > 0时的积分轮廓线在p > 0时正好低于奇异点，而在p < 0时正好高于奇异点。考虑到地震波在半空间内的轻微衰减(这是我们在物理上很可能需要的)，这种轮廓可能是合理的，在这种情况下，极点进入复杂p平面的第一象限和第三象限。分支线从$α^{−1}_L， β^{−1}_L$切断是不重要的，只需

$$\mathrm{Im}(\omega{q}_{\alpha{L}})\geq0,\quad\mathrm{Im}(\omega{q}_{{\beta}{L}})\geq0\tag{7.81}$$

都保持在实p轴上。因此，我们按照兰姆(1904)的方法，取平行于虚p轴的切面

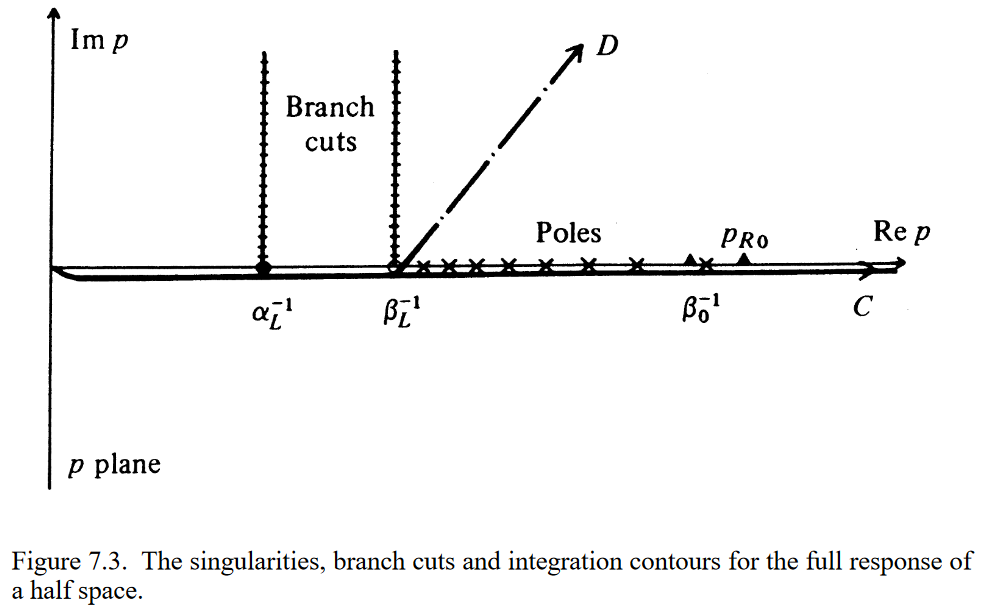
计算式(7.75)或式(7.77)的最直接方法是沿着实p轴直接进行数值积分，但对于完全弹性介质，轮廓上极点的存在是这种方法的主要障碍.然而，如果我们将(7.77)中的积分轮廓变形到上半平面到D，我们可以从$β^{−1}_L$右侧的所有极点中提取极性残量贡献。无穷远处的收敛性由$H^{(1)}_m(ωpr)$的性质保证。对于这种变形，位移谱给出为轮廓积分和残差级数的和。

$$\begin{gathered} \bar{\mathbf{u}}_{P}({r},{m},0,{\omega}) =\frac12\omega|\omega|\{\int_{{D}}\mathrm{d}p\mathrm{~p}{w}_0^{{T}}(p,{m},\omega){T}_{{m}}^{(1)}(\omega\text{pr})\} \\ +\pi\mathrm{i}\omega^2\sum_{j=0}^{{N}(\omega)}{p}_j\mathrm{Res}_j[{w}_0^\mathsf{T}{T}_{m}^{(1)}] \end{gathered}\tag{7.82}$$

即使在中等频率下，模态残差贡献的N(ω)数也会变得非常大(参见图11.3)，并且定位所有极点是一个主要的计算问题。慢度最大的极点对通常被认为是表面波列的主要贡献，具有相对较低的群速度。慢度较小模态的和只是通过模态干涉合成S体波相位。当残差和只占实p轴的一部分时，S波尾可以得到很好的结果(Kerry, 1981)，并且通过迫使αL、βL非常大，即使p波也可以被合成(Harvey, 1981)。我们将在第11章更详细地考虑这种模态求和方法

(7.82)中的轮廓积分包括从$−\infty$到$β^{−1}_L$的实轴慢度积分，然后是进入第一象限的线段，其中$H^{(1)}_m (\omega pr)$是复p的衰减函数。对于大范围r，负慢度的贡献非常小，经常被忽略。Wang和Herrmann(1980)使用了这种方法，他们将轮廓D进一步变形，使其沿着分支切口的两侧，沿着虚p轴和实p轴到$\beta^{-1}_l$。他们沿着实轴和虚轴使用了不同的数值积分方案。

我们刚刚描述的轮廓变形过程的另一种替代方法是安排将响应中的极点移出积分轮廓。对于衰减介质，极点将位于远离实际p轴的第一象限和第三象限，尽管它们对积分轮廓的影响强烈。在大多数应用中，我们预计地震波在传播过程中至少会发生一些损耗，因此引入较小的损耗因子是非常合理的。Kind(1978)构造了衰减介质对垂直点力激励的完整响应，但在(7.77)中采用了Hankel函数的渐近形式，因此排除了近场效应;他还将p上的数值积分限制在覆盖感兴趣的主体波和表面波相位的正慢度带内。

在原点处，Jm(ωpr)贝塞尔函数保持良好的性能，因此当试图计算半空间的完全响应时，使用驻波表达式(7.75)具有优势。如果需要相当宽的频带，对于最短范围和最低频率，ωpr可以相当小，因此希望在整个参数范围内使用高精度近似Jm(x)，例如，通过Kennett(1980)中的切比雪夫多项式。对于宽带信号，衰减引起的速度色散(1.19)、(1.25)的影响会变得非常显著，在计算介质响应时应严格考虑。当损耗因子较小时$(Q^{−1}_\alpha， Q^{−1}_\beta < 0.03)$，传输距离小于500 km时，忽略色散引起的脉冲畸变很小;这与O 'Neill & Hill(1979)的结果一致，他们表明，在通过$Q^{−1}_\alpha > 0.01$的区域传播600公里时，脉冲形式会发生显著变化。

根据反射矩阵表示法(7.46)，z = zS处一般点源的理论地震记录的构建分三个阶段进行。对于曲面接收器，我们构造矩阵算子

$$\mathbf{Z}({p},\omega)=\mathbf{W}_{{U}}^{\mathrm{fS}}[\mathbf{I}-\mathbf{R}_{{D}}^{\mathrm{SL}}\mathbf{R}_{{U}}^{\mathrm{fS}}]^{-1}\tag{7.83}$$

为响应的P-SV和SH部分。Z(p， ω)与角阶m和源类型无关，因此对于任何源深度只需要形成一次。反射矩阵$R^{SL}_D(p, \omega)$适用于均匀层叠或分段光滑结构，可以递归地构建，从zL到源级，如第6章所讨论的。同样，位移矩阵$W^{fS}_U$和自由表面反射矩阵$R^{fS}_U$可以通过从自由表面向下到水平zS来计算。

如果我们能够假设源矩张量$M_{ij}$中的所有元素具有相同的时间依赖性M(t)，则可以简化计算。然后，我们可以从源项中提取相应的谱$\bar M(ω)$;在固定慢度p下，源辐射项$\Sigma U$和$\Sigma D$与频率无关，但通过源的特性取决于方位角阶m。对于每个角阶m，我们现在可以以慢度p和频率ω 构造变换向量w0

$$w_0({p},{m},\omega)=\mathbf{Z}({p},\omega)[\mathbf{R}_{\mathrm{D}}^{\mathrm{SL}}({p},\omega)\mathbf{\Sigma}_{\mathrm{D}}({p},{m})+\mathbf{\Sigma}_{\mathrm{U}}({p},{m})]\bar{{M}}(\omega)\tag{7.84}$$

从水平波数k到慢度p的变量变化给出了$\omega^2 \bar M(\omega)$的有效源谱。我们记得，无界介质中的远场位移是由矩时间函数的导数控制的，因此指定矩速率谱$i\omega (\omega)$通常是有利的。对于具有时间函数$\mathcal E(t)$的点力的激励，我们用$(i\omega)^{−1}\bar{\mathcal E}(ω)$代替式(7.84)中的矩谱。

对于每个方位分量，我们现在必须在p上进行数值积分，以产生范围r内位移的三个分量的频谱。对于由一般矩张量指定的源，我们需要五个方位阶，因此当使用矢量谐波的原始形式包括近场项时，我们对每个范围有15个慢度积分(2.56)。角项的最后求和得到从震源出发的给定方位的三分量地震图。如果可以使用谐波的渐近形式(7.79)，我们只需要对每个位移进行一次积分。不幸的是，在适当的情况下，即在中等范围内，使最快的体波和最慢的表面波之间的时间间隔不是太大，是适合尝试计算完整的合成地震记录的，而在这种情况下，渐近近似是勉强足够的.

(7.75)中的慢度积分有无穷上限，但数值积分需要截断。对于2 Hz左右的频率，Kennett(1980)从原点积分到慢度$(0.85 \beta_0)^{−1}$，对于表面剪切波速$\beta_0$。这种慢度远远超过了基本瑞利模的高频渐近值$p_{R0}$。在较低的频率下，将计算扩展到稍大的慢度是有利的。

式(7.75)中的被积函数有一个相对不讨人喜欢的特点。通过$J_m(\omega pr)$的存在，矢量谐波是振荡的:$w_0(p, m， ω)$绝不是平滑的，特别是当积分路径经过从实轴偏移的极点肩部时，由于包含衰减。最简单的数值积分方法是将慢度积分分成几部分，在每一部分中使用梯形规则，并根据被积函数的特点选择面板间距..例如，对于$p > β^{-1}_L$，将使用更精细的采样。另一种方法是将Filon(1928)的方法修改为贝塞尔函数积分，并尝试在每个积分面板上对$w_0(p, m， ω)$进行多项式拟合。然后将积分计算为$\int{dx}{x^p}{J}_{m}({kx})$形式的贡献之和。

对于较大的ωpr，需要在慢度下进行相当精细的采样，才能很好地表示被积函数。因此，在没有过多计算的情况下，在给定范围内存在频率的有效上限，当我们寻求保持给定精度时，在给定频带内存在最大范围。

在非常低的频率下，基波瑞利模式几乎不受分层损耗因子的影响，因此需要非常细的慢度间隔来处理积分路径上的近极。修改积分轮廓以明确地提取基本瑞利模极可能是值得的。如果我们使用(7.75)，这将需要从极点左侧开始的两个额外线段:一个进入p平面的上半部分，与H(1) m (ωpr)相关，另一个进入下半部分，取决于H(2) m (ωpr)。

Cormier(1980)使用了一个分段平滑模型的等价表示(7.77)。通过变形积分的轮廓，他从基本瑞利模式中分离出了剩余贡献，并采取了一条进入p平面上半部分的路径，以排除非常小的慢度，从而避免了原点的奇点。当使用驻波表达式(7.75)时，我们知道整个响应可以用传出函数来表示，任何明显传入波的大小提供了对任何数值积分精度的非常有用的检查。

同时构造地震记录的横波和横波部分是可取的，因为这样可以正确地计算近场对水平分量地震记录的贡献。Wang和Herrman(1980)已经表明，忽略P-SV波或SH波的近场项会产生非因果的、非传播的到达，当这两种贡献都包括在内时，它们会相互抵消。对于长周期波，在中等范围内，近场贡献对计算波形有显著影响。例如，在一个简单的地壳模型中，完整计算的表面波和只包含远场项的表面波在80公里范围内显示出明显的差异。

在慢度积分和方位求和之后，我们就得到了接收机位置的地震记录频谱。最后的时域积分通常通过在一组离散频率上使用快速傅里叶变换(Cooley & Tukey 1965)来完成。实际记录设备的有限带宽设置了频率的上限，并且必须在奈奎斯特频率以下进行变换。变换后得到的时间序列长度固定，具有循环性质。因此，有时间“混叠”的可能性，在分配的时间间隔结束后到达的能量被包裹在地震记录的早期部分。

对于完整的地震记录，我们有很长的信号持续时间，直到表面波列的末端;为了产生如此长的时间间隔，我们需要非常精细的频率间隔。为了在固定的时间间隔内跟踪不同范围的到达，通过将r处的频谱乘以exp(- iωpredr)来计算u(r, t - predr)是方便的(Fuchs & M ø uller 1971)。选择减速速度是为了最方便地限制到达。因此，如果在每个频率将慢度积分分成若干部分，则可以使用不同的简化慢度来计算每个部分的时间序列。最后的地震记录可以通过对具有适当时间延迟的剖面的时间序列进行叠加得到(Kennett 1980)。

0阶贝塞尔函数，通常记作$J_0(x)$，是贝塞尔函数中的一种特殊函数。它的表达式可以通过级数展开或者积分表示得到。

一种常见的定义是通过级数展开： [ J_0(x) = 1 - \frac{x^2}{22 \cdot 1!} + \frac{x^4}{24 \cdot 2!} - \frac{x^6}{26 \cdot 3!} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n}{(n!)2} \left(\frac{x}{2}\right)^{2n} ]

另外，$J_0(x)$ 还可以通过积分形式表示为： [ J_0(x) = \frac{1}{\pi} \int_{0}^{\pi} \cos(x \sin \theta) \, d\theta ]

这些表达式都可以用来计算贝塞尔函数的值。