概括

RAPID GENERATION OF SYNTHETIC SEISMOGRAMS IN LAYERED MEDIA BY VECTORIZATION OF THE ALGORITHM

反射率法论文解读

传播矩阵概念

参考链接： https://www.youtube.com/watch?v=BX_-1ei12sU&list=LL&index=10&t=274s

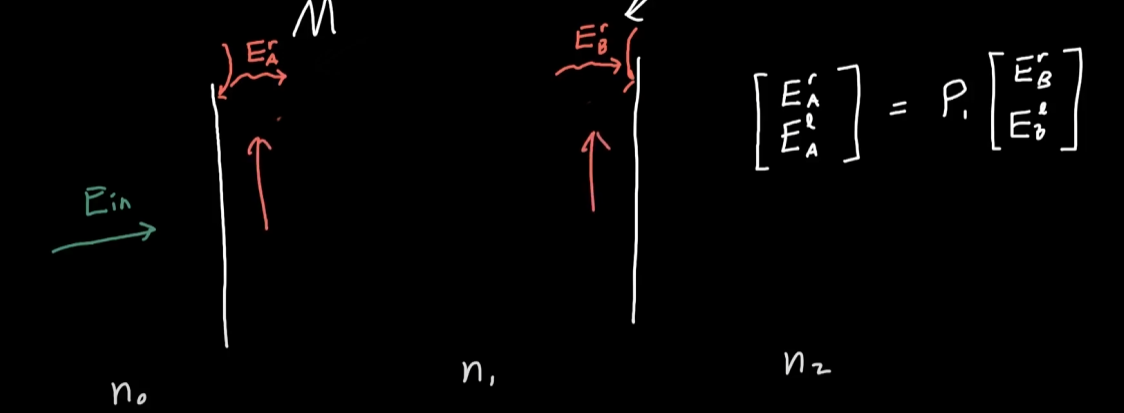
A点与B点的电场变化: $E_A \to E_B$ 的过程用 $\left[\begin{matrix} E_A^r\\ E_A^l \end{matrix}\right] = P \left[\begin{matrix} E_B^r\\ E_B^l \end{matrix}\right]$ 表示, 其中上标表示向右传播与向左传播

根据公式$E_B(x) = E_A(x+L_{AB})$

且$E_A(x) = E_0e^{j(\omega t-kx)}$ k为波传播方向, 所以$E_A(x+L)=E_0e^{j(\omega t-kx)}e^{-jkL}$

结合方向得到

$$\left[\begin{matrix} E_A^r\\ E_A^l \end{matrix}\right] = \left[\begin{matrix}{} e^{+jkl}&0\\ 0&e^{-jkl} \end{matrix}\right] \left[\begin{matrix} E_B^r\\ E_B^l \end{matrix}\right]$$

反射率法同理

定义初始六元速度

$$\vec v = \begin{bmatrix} 1&0&0&0&0&0 \end{bmatrix}^T$$

通过传播矩阵乘法向上延拓至第0层得到

$$\vec v = Q_0Q_1\dotsb Q_{N-1}\vec v_N$$

$v_0$定义

$$v_{0}=[\Delta,-R_{PS}\Delta,-R_{SS}\Delta,R_{PP}\Delta,R_{SP}\Delta, \text{det}R\Delta]$$

每个波传播矩阵Q，是一个界面矩阵F和一个层穿越矩阵E的乘积

$$Q_n = E_nF_n$$

其中

$$E_n = \text{diag}\begin{bmatrix} e^{-i\omega h_n(q_n^P+q_n^S)}&1&e^{-i\omega h_n(q_n^P-q_n^S)}&e^{i\omega h_n(q_n^P-q_n^S)}&1&e^{-i\omega h_n(q_n^P+q_n^S)} \end{bmatrix}$$

$$F_n = T_n^{-1}T_{n+1}(穿越指T_n \to T_{n+1}的过程,即T_nF_n = T_{n+1})$$

P, SV, SH波

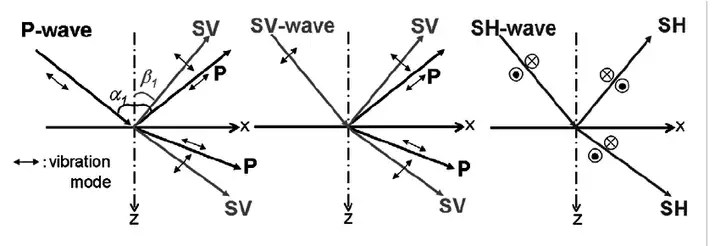
字母含义

$p$ : 水平慢度 $q$: 垂直慢度 P31 $W$ 位移矩阵 $T$ 牵引力矩阵 $m$ 位移 $n$ 牵引力

$P$ 应力位移矢量的传播矩阵, $Q$ 波的传播矩阵(界面系数矩阵)

Chapter 2

传播不变量

对基本B矩阵进行划分，以显示位移和应力元素，这样我们就写了

$$\mathbf{B}=\begin{bmatrix}\mathbf{W}_1&\mathbf{W}_2\\\mathbf{T}_1&\mathbf{T}_2\end{bmatrix}\tag{2.67}$$

用位移矩阵W和与之相关的牵引矩阵T表示。对于P-SV系统W将是一个2 × 2矩阵，其列可以被认为是二阶系统(2.31)的独立解，并且牵引矩阵如(2.33)中所示，$\omega T = A \partial_z W + \omega p B W$。在SH的情况下，W和T只是位移和牵引元素W, T。任何特定的应力-位移向量都可以通过取B列的线性组合来创建，有常数c: b = Bc

通过扩展我们对传播不变量的处理，我们可以建立一个基本矩阵逆的一般形式。对于位移矩阵W1和W2，我们引入该矩阵

$$<W_1,W_2>=W_1^\mathrm{T}T_2-T_1^\mathrm{T}W_2\tag{2.68}$$

中的第i项是由W1的第i列和W2的第j列构造的表达式(2.36)。对于SH波(2.68)与(2.36)没有区别，但对于P-SV波是一个2 × 2矩阵。由于(2.68)中的每个条目都与深度无关，所以也是如此，并且我们有一个矩阵传播不变量。从定义(2.68)

$$<W_1,W_2>^{\mathsf{T}}=-<W_2,W_1>\tag{2.69}$$

Chapter3 P37

3.1 均匀介质

对于频率为ω，慢度为p，角阶为m的圆柱形波，我们引入了将应力-位移矢量b与新矢量v连接起来的变换

$$b=Dv$$

选择矩阵D来给出v随z的演化的简单形式

$$\vdots$$

$$v(z)=\exp[i\omega(z-z_0)\Lambda]v(z_0)=Q(z,z_0)v(z_0)\tag{3.10}$$

Q为传播矩阵,取决于当前深度$z$和参考深度$z_0$, 对于P-SV波

$$Q_P(h,0)=\operatorname{diag}[\mathrm{e}^{-\mathrm{i}{\omega}{q}_{\alpha}{h}},\mathrm{e}^{-\mathrm{i}{\omega}{q}_{\beta}{h}},\mathrm{e}^{\mathrm{i}{\omega}{q}_{\alpha}{h}},\mathrm{e}^{\mathrm{i}{\omega}{q}_{\beta}{h}}]\tag{3.11}$$

对于SV波

$$Q_H(h,0)=\operatorname{diag}[\mathrm{e}^{-\mathrm{i}{\omega}{q}_{\beta}{h}},\mathrm{e}^{\mathrm{i}{\omega}{q}_{\beta}{h}}]\tag{3.12}$$

对于P - SV波，我们设定

$$\mathbf{v_P}=[{P_U},{S_U},{P_D},{S_D}]^{T}\tag{3.15}$$

对于SH波

$$\mathbf{v_H}=[{H_U},{H_D}]^{T}\tag{3.16}$$

通过引入对应于上行波和下行波的分划来总结波矢v

$$\mathbf{v}=[{v_U},{v_D}]^{T}\tag{3.17}$$

在均匀介质中，系数矩阵A是常数，因此特征向量矩阵D与z无关, 将b公式代入可得

$$b(z) = D \exp[i\omega(z-z_0)\Lambda]D^{-1}b(z_0)\tag{3.19}$$

故b的传播矩阵为

$$\mathbf{P}(z,z_0)=\exp[\omega(z-z_0)\mathbf{A}]=\mathbf{D}\exp[\mathrm{i}\omega(z-z_0)\boldsymbol{\Lambda}]\mathbf{D}^{-1}\tag{3.20}$$

特征向量矩阵D在可以看成是在参考水平$z_{ref}$下评估的基本矩阵，因此其列可以被识别为对应于不同波型的"基本"应力-位移向量。

对于P-SV波

$$\mathbf{D}_{\mathrm{P}}=[\epsilon_{\alpha}\mathbf{b}_{\mathrm{U}}^{\mathrm{P}},\epsilon_{\beta}\mathbf{b}_{\mathrm{U}}^{\mathrm{S}};\epsilon_{\alpha}\mathbf{b}_{\mathrm{D}}^{\mathrm{P}},\epsilon_{\beta}\mathbf{b}_{\mathrm{D}}^{\mathrm{S}}]\tag{3.22}$$

对于SH波

$$\mathbf{D}_{\mathsf{H}}=[\epsilon_{\mathsf{H}}\mathbf{b}_{\mathsf{U}}^{\mathsf{H}};\epsilon_{\mathsf{H}}\mathbf{b}_{\mathsf{D}}^{\mathsf{H}}]\tag{3.24}$$

$\epsilon$为尺度参数,可以调整使这些参数在一个量纲上。对这些b矢量进行归一化处理很方便，使得在完全弹性介质中，传播波在z方向上的每个b矢量携带相同的能量通量。

p41 特征向量矩阵D是基本矩阵的一种特殊情况，我们可以通过将D写成分块形式来显示它作为变换的作用

$$\mathbf{D}=\begin{bmatrix}m_\mathrm{U}&m_\mathrm{D}\\n_\mathrm{U}&n_\mathrm{D}\end{bmatrix}\tag{3.36}$$

$m_U$表示上行波矢量$v_U$转为位移的变换算子， $m_D$表示下行波矢量$v_D$转为位移的变换算子，同理$n_U$和$n_D$表示波矢量转化为上行下行应力的算子

对于P-SV波

$$\begin{aligned} &m_{\mathrm{U,D}} =\begin{bmatrix}\mp\mathrm{i}{q}_\alpha\epsilon_\alpha&{p}\epsilon_\beta\\{p}\epsilon_\alpha&\mp\mathrm{i}\mathfrak{q}_\beta\epsilon_\beta\end{bmatrix} \\ &n_{\mathrm{U,D}} =\begin{bmatrix}\rho(2\beta^2p^2-1)\epsilon_\alpha&\mp2\mathrm{i\rho\beta}^2\text{рq}_\beta\epsilon_\beta\\\mp2\mathrm{i\rho\beta}^2\text{рq}_\alpha\epsilon_\alpha&\rho(2\beta^2\text{p}^2-1)\epsilon_\beta\end{bmatrix} \end{aligned}\tag{3.37}$$

对于SH波

$$m_{\mathrm{U,D}}=\beta^{-1}\epsilon_\beta,\quad n_{\mathrm{U,D}}=\mp\mathrm{i\rho\beta}q_\beta\epsilon_\beta\tag{3.38}$$

通过构造传播不变量可以得到方便的得到$D^{-1}$ P42

$$\mathbf{D}^{-1}=\mathrm{i}\begin{bmatrix}-\mathbf{n}_\mathrm{D}^\mathrm{T}&\mathbf{m}_\mathrm{D}^\mathrm{T}\\\mathbf{n}_\mathrm{U}^\mathrm{T}&-\mathbf{m}_\mathrm{U}^\mathrm{T}\end{bmatrix}\tag{3.40}$$

在得到$D$和$D^{-1}$后, 根据(3.20)来构造均匀介质中应力-位移传播子的表达式。对于P - SV波

$$\mathbf{P}_{{P}}({h},0)=\mathbf{D}_{{P}}\operatorname{diag}[\mathrm{e}^{-\mathrm{i}{\omega}{q}_{\alpha}{h}},\mathrm{e}^{-\mathrm{i}{\omega}{q}_{\beta}{h}},\mathrm{e}^{\mathrm{i}{\omega}{q}_{\alpha}{h}},\mathrm{e}^{\mathrm{i}{\omega}{q}_{\beta}{h}}]\mathbf{D}_{{P}}^{-1}\tag{3.41}$$

传播子的划分PWW，PWT，PTW，PTT在P42式(3.42)

对于SH波

$$\mathbf{P}_H(h,0)=\begin{bmatrix}\mathcal{C}_\beta&(\rho\beta^2)^{-1}\mathcal{S}_\beta\\-\rho\beta^2\mathcal{q}_\beta^2\mathcal{S}_\beta&\mathcal{C}_\beta\end{bmatrix}\tag{3.44}$$

借助D及其逆的表达式( 3.36 )和( 3.40 )，我们可以将均匀层传播子表示为上行和下行贡献之和

$$\mathbf{P(h,0)=i}\begin{bmatrix}-\mathbf{m_uE_un_D^T}&\mathbf{m_uE_um_D^T}\\-\mathbf{n_uE_un_D^T}&\mathbf{n_uE_um_D^T}\end{bmatrix}+\mathrm{i}\begin{bmatrix}\mathbf{m_DE_Dn_U^T}&-\mathbf{m_DE_Dm_U^T}\\\mathbf{n_DE_Dn_U^T}&-\mathbf{n_DE_Dm_U^T}\end{bmatrix}\tag{3.45}$$

其中对角矩阵$E_D$是下行波的相位收入，对于P-SV波

$$E_D=\text{diag}[e^{i\omega q_\alpha h},e^{i\omega q_\beta h}] \quad and \quad E_U=E_D^{-1}$$

3.2 平滑变化的介质

3.3 一致近似