生成对抗网络

AVO Inversion Based on Closed-Loop Multitask Conditional Wasserstein Generative Adversarial Network

基于闭环多任务条件Wasserstein生成对抗网络的avo反演

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=10078923&tag=1

摘要

标记数据不足的情况下，基于神经网络的地震反演结果精度下降，甚至低于基于传统反演方法的反演结果。此外，基于神经网络的地震反演结果普遍存在横向不连续性。针对这些问题，本文提出了一种基于闭环多任务条件Wasserstein生成对抗网络( CMcWGAN )的AVO反演方法，即基于生成对抗网络( GAN )的AVO反演方法。这可以同时准确反演三个弹性参数，同时，利用弹性参数的低频信息作为条件输入，缓解了反演结果的横向不连续问题。相较于传统AVO反演，具有更高的精度和鲁棒性

INTRODUCTION

AVO反演可以有效地预测地下介质的弹性参数，为储层预测和流体识别提供可靠的理论依据

AVO反演方法的发展：

• Zoeppritz方程及其近似
• 加权叠加法实现线性AVO反演
• 贝叶斯网络
• 基于L1范数的似然函数和全变差( TV )正则化约束
• 基于马尔科夫随机场( MRF )的正则化
• L曲线和广义交叉验证( GCV )
• 方向全变分( DTV )正则化
• 机器学习
• 人工神经网络
• 物理引导神经网络( PGNN )
• 闭环CNN
• 生成对抗网络GAN

本文提出了一种基于闭环多任务条件WGAN ( CMcWGAN )的反演方法，它将闭环框架和基于GAN的网络相结合，设计了GAN的结构，实现了3个弹性参数同时反演，可以实现多任务学习。此外，为了提高网络训练的鲁棒性，使用Wasserstein距离代替交叉熵( CE )作为损失函数，使用cGAN通过引入低频信息到网络缓解横向不连续性。我们的方法具有更高的反演精度和更好的抗噪性。

CMcWGAN Framework and Neural Network Structure

CMcWGAN由两个子网络组成：反演网络和正演网络

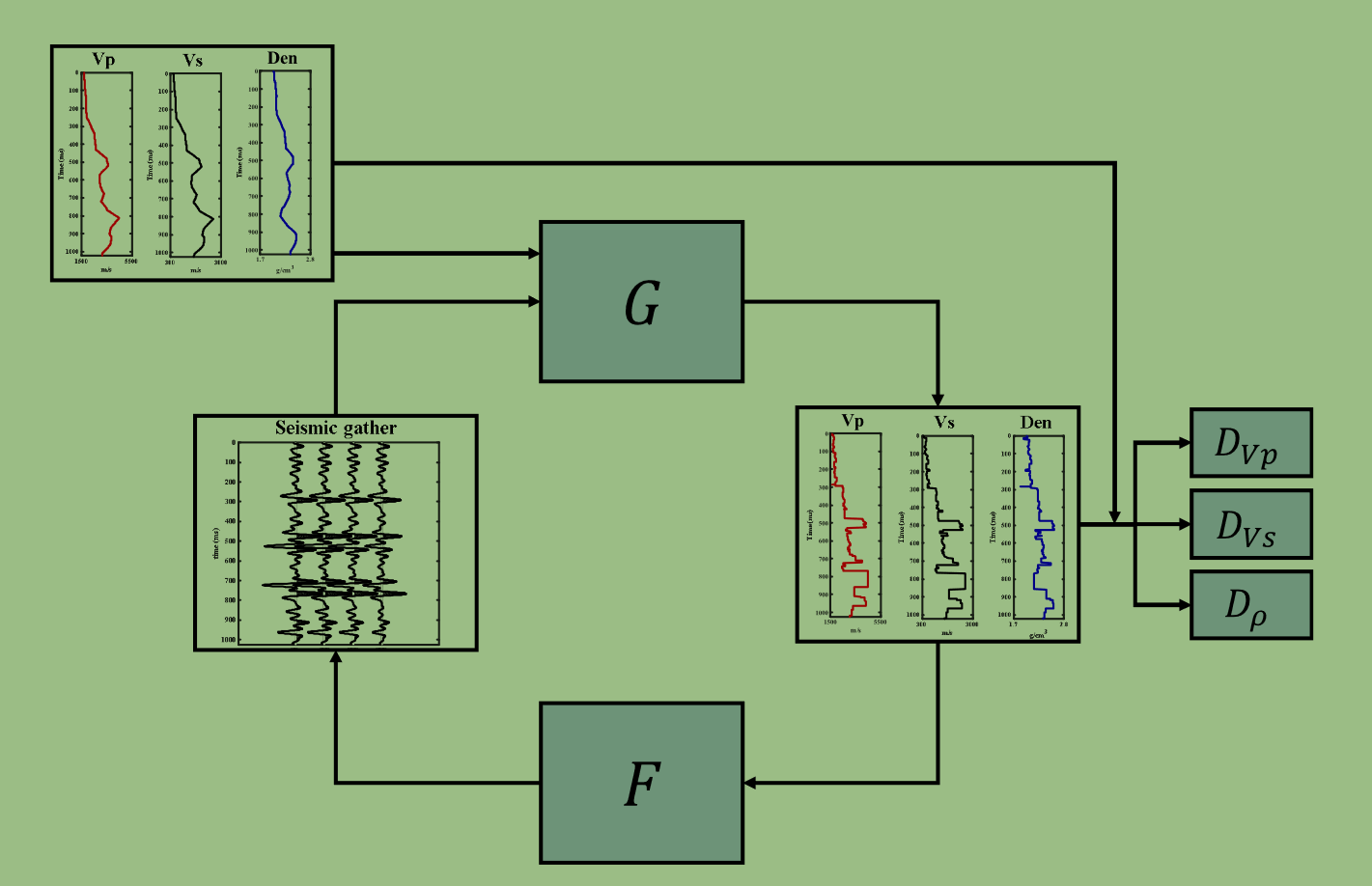
G为反演网络生成器。DVp、DVs和Dρ分别为纵波速度、横波速度和密度对应的判别器。F为正演网络

G结构如下：

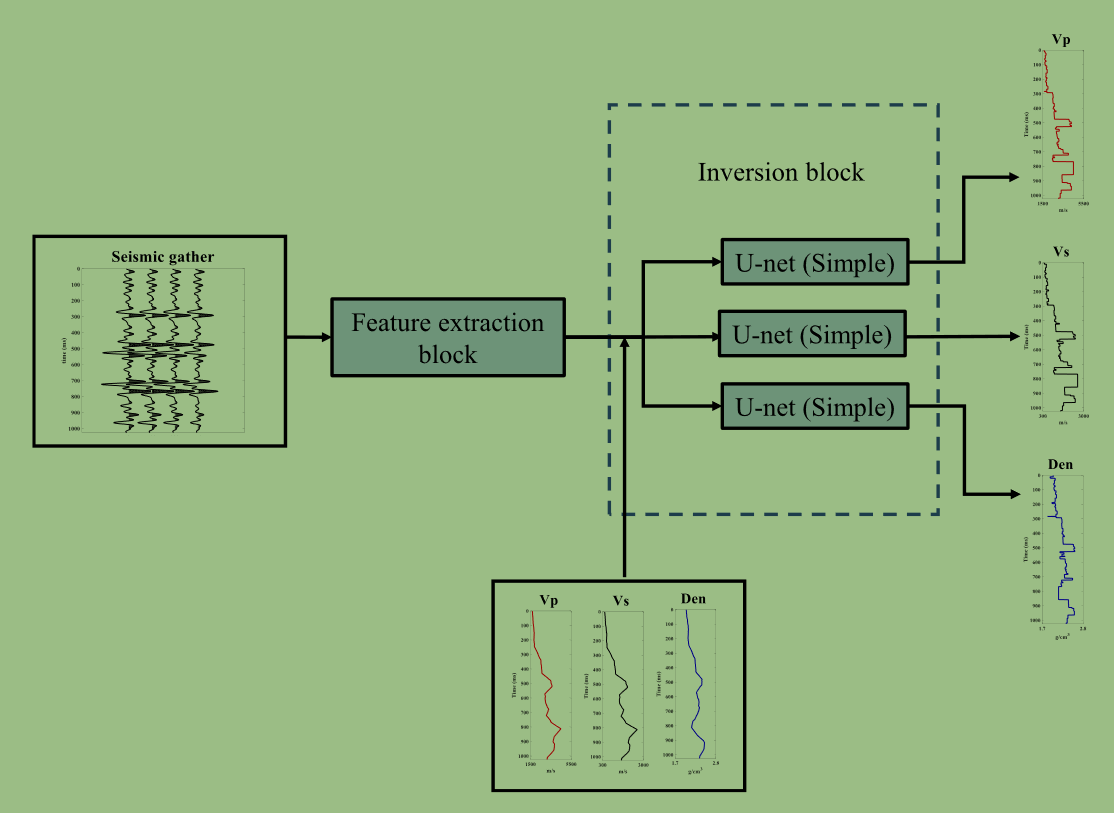
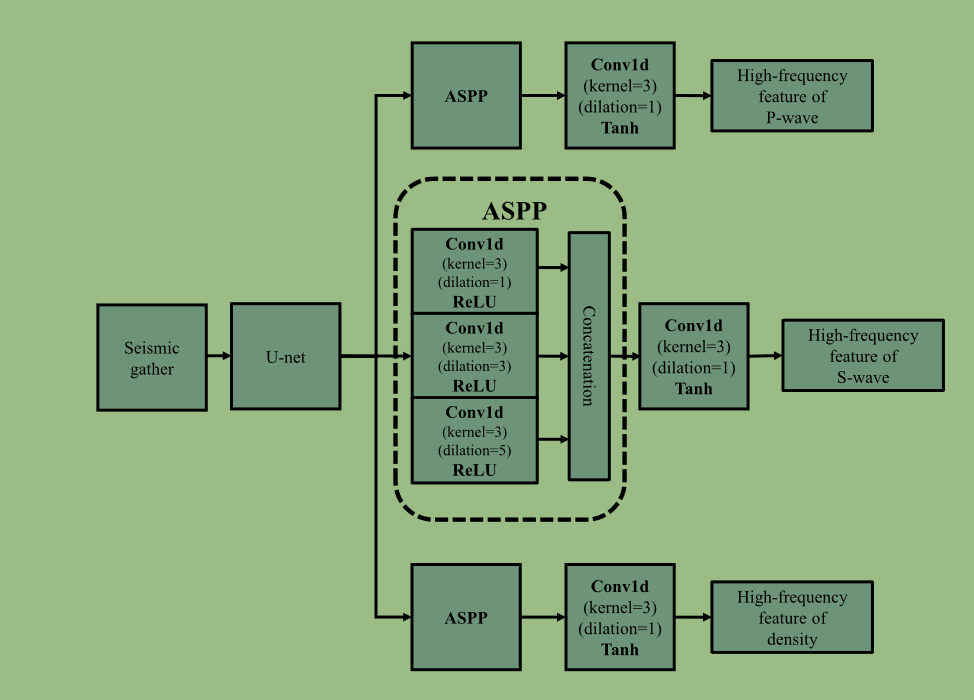
feature block其中特征提取block结构为

U-net结构

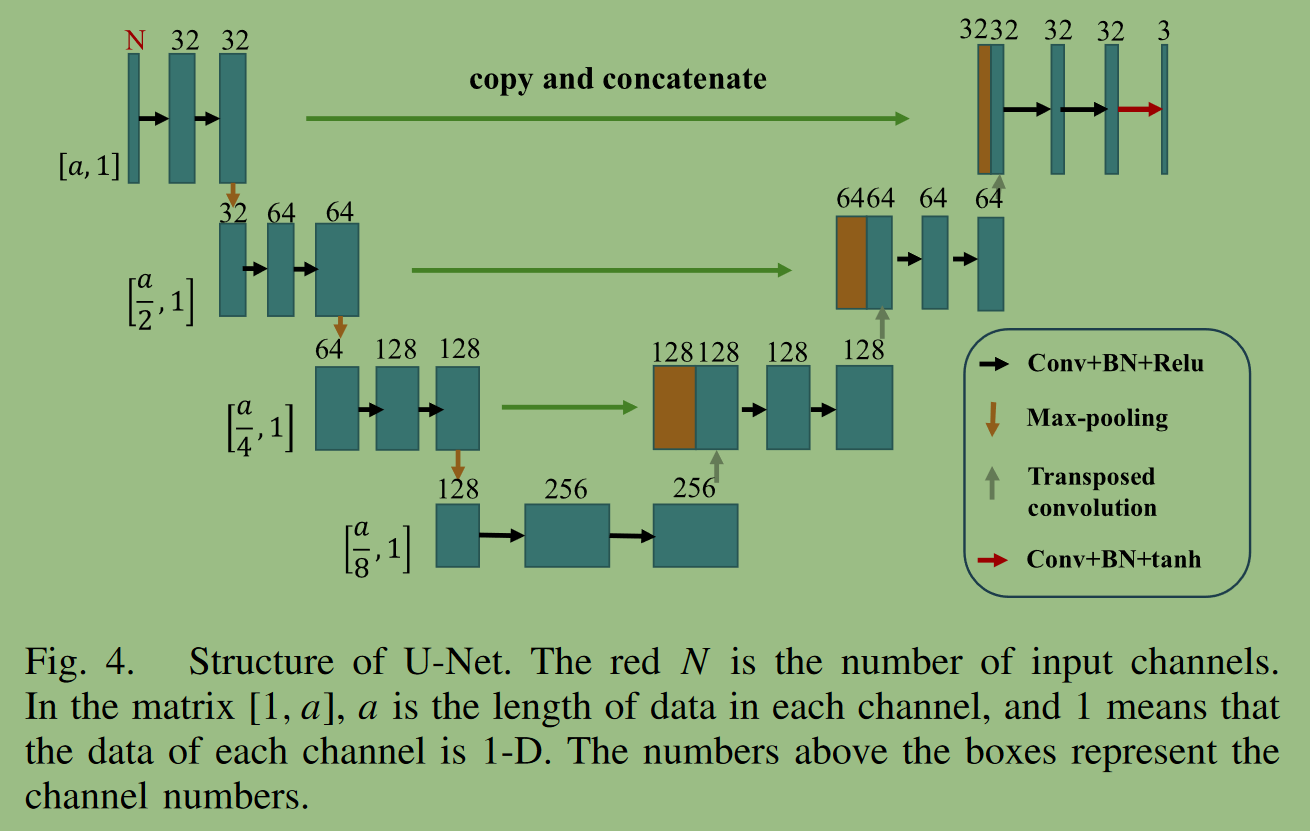
N代表入射角，a代表数据长度

将每个下采样和对应的上采样特征的数据进行跳跃拼接，融合数据的浅层特征和深层特征。这是解决传统全卷积神经网络梯度消失问题的有效方法

在ASPP结构中，较小的核尺寸可以捕获数据的高频内容，因此，ASPP的核尺寸均为3×1，通过空洞卷积增大感受野，捕获多个尺度的特征。

在G结构中，inversion block使用了三个1-D U-net，该块的U - Net比特征提取块具有更浅的深度和更简单的结构。参考cGAN的理论，这里的三个unet均为双通道输入，一个为特征提取到的高频信息，另一个为预设低频信息。

discriminator判别器结构

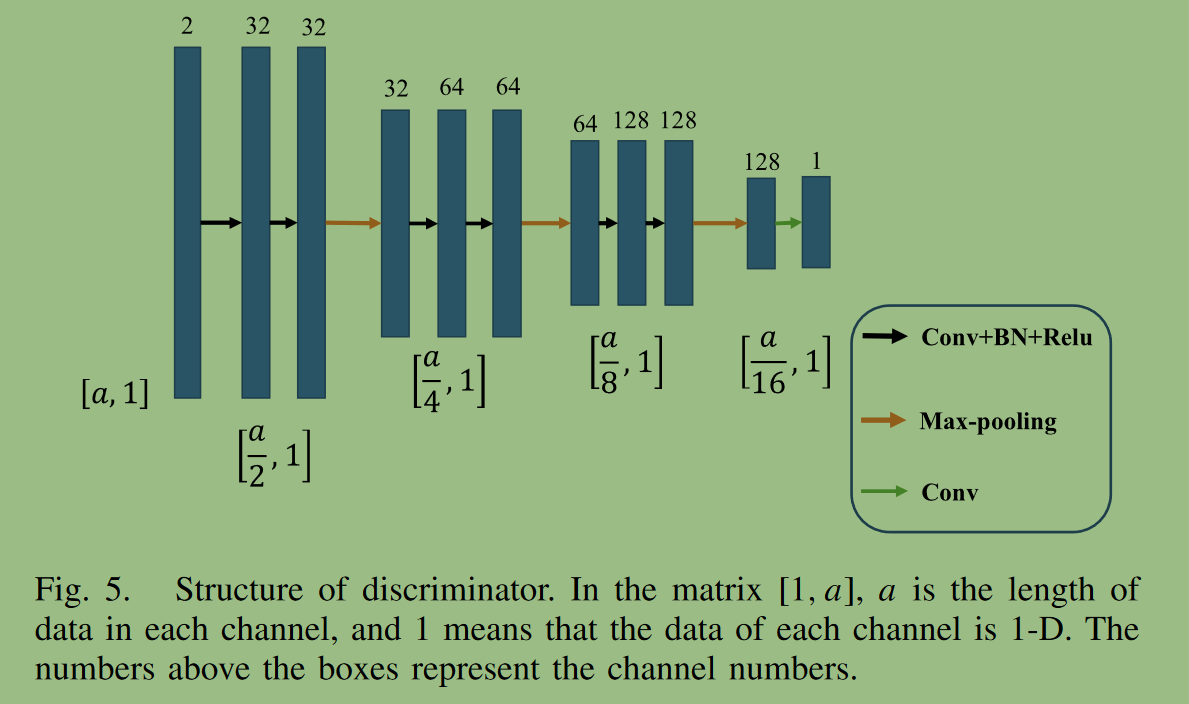
判别器为3个结构相同的网络，本文采用一维马尔科夫判别器代替传统的GAN判别器进行多任务cGAN。马尔科夫判别器的输出是一个矩阵或向量，而不是传统GAN中的0或1输出。这意味着输出的每个元素对应输入数据的一个补丁。这样可以增强反演结果中高频细节的刻画。判别器同样是低频高频双通道输入，最终输出大小为输入的1/16

F正演网络

我们在AVO反演中使用神经网络代替基于物理的方程进行地震正演。由于U - Net在地震正演方面也具有良好的性能，因此我们将U - Net作为AVO正演网络(F)，实现弹性参数到地震角道集的映射。F的结构如上Unet。它通过三个通道将三个弹性参数分别输入网络；所以N=3。最终得到角道集

Loss function

三个判别器的损失函数

$$\begin{aligned} & L_{V p}^d=\frac{1}{m} \sum_i^m\left[-D_{V p}\left(V p^{\text {label }} \mid V p^{\text {low }}\right)\right. \left.+D_{V p}\left(G\left(S \mid V p^{\text {low }}\right) \mid V p^{\text {low }}\right)+\lambda \mathrm{gp}_{V p}\right] \\ & L_{V s}^d=\frac{1}{m} \sum_i^m\left[-D_{V s}\left(V s^{\text {label }} \mid V s^{\text {low }}\right)\right. \left.+D_{V s}\left(G\left(S \mid V s^{\text {low }}\right) \mid V s^{\text {low }}\right)+\lambda \mathrm{gp}_{V s}\right] \\ & L_\rho^d=\frac{1}{m} \sum_i^m\left[-D_\rho\left(\rho^{\text {label }} \mid \rho^{\text {low }}\right)\right. \left.+D_\rho\left(G\left(S \mid \rho^{\mathrm{low}}\right) \mid \rho^{\mathrm{low}}\right)+\lambda \mathrm{gp}_\rho\right] \\ & \mathrm{gp}=E_{\tilde{x}, y}\left[\left(\left\|\nabla_{\tilde{x}} D(\tilde{x}, y)\right\|_2-1\right)^2\right] \\ & \tilde{x}=t x+(1-t) G(y) \\ \end{aligned}$$

其中，m为标记数据的个数，S为有标注数据的地震角度道集，gp为梯度惩罚，满足1-Lipschitz约束，$\lambda$为约束系数在gp的表达式中，y是作为生成器输入的原始数据。$\nabla_{\tilde{x}}$是沿$\tilde{x}$方向的梯度计算。$\tilde{x}$随机采样于在x作为标签和对应的生成数据G (y)之间的直线上。

生成器的损失函数

$$\begin{aligned} & L^g=\frac{1}{m} \sum_i^m\left[-D_{V_p}\left(G\left(S \mid V p^{\text {low }}\right) \mid V p^{\text {low }}\right)\right. -D_{V s}\left(G\left(S \mid V s^{\text {low }}\right) \mid V s^{\text {low }}\right) \\ & \left.-D_\rho\left(G\left(S \mid \rho^{\text {low }}\right) \mid \rho^{\text {low }}\right)\right] \text {. } \\ \end{aligned}$$

我们使用了循环一致损失函数，G和F的互为输入输出，因此，G和F操作的数据都是闭环的，相比之下，仅由单个网络G或F操作的数据意味着开环。此外，根据AVO反演的需求，对循环一致损失函数进行了改进。此外，我们使用平均绝对误差(MAE)代替均方误差(mse)作为损失函数，以提高训练的鲁棒性。开环损失函数如下

$$\begin{aligned} & L_{\text {open }}^1=\frac{1}{m} \sum_i^m \| G\left(S \mid V p^{\text {low }}\right)-V p^{\text {label }} \mid +\left|G\left(S \mid V s^{\text {low }}\right)-V s^{\text {labcl }}\right| \\ & \left.+\left|G\left(S \mid \rho^{\text {low }}\right)-\rho^{\text {labcl }}\right|\right] \\ & L_{\mathrm{open}}^2=\frac{1}{m} \sum_i^m\left[\left|F\left(V p^{\text {label }}, V s^{\text {labcl }}, \rho^{\text {label }}\right)-S\right|\right] . \\ & \end{aligned}$$

闭环损失函数由正演地震数据的损失，反演三参数的损失，未标注数据的正演损失组成

$$\begin{align} & L_{\text {close }}^1=\frac{1}{m} \sum_i^m\left[\left|F\left(G\left(S \mid V p^{\text {low }}\right), G\left(S \mid V s^{\text {low }}\right), G\left(S \mid \rho^{\text {low }}\right)\right)-S\right|\right] \\ & L_{\text {close }}^2=\frac{1}{m} \sum_i^m\left[\left|G\left(F\left(V p^{\text {label }}, V s^{\text {label }}, \rho^{\text {label }}\right) \mid V p^{\text {low }}\right)-V p^{\text {label }}\right|\right] \\ & L_{\text {close }}^3=\frac{1}{m} \sum_i^m\left[\left|G\left(F\left(V p^{\text {label }}, V s^{\text {label }}, \rho^{\text {label }}\right) \mid V s^{\text {low }}\right)-V s^{\text {label }}\right|\right] \\ & L_{\text {close }}^4=\frac{1}{m} \sum_i^m\left[\left|G\left(F\left(V p^{\text {label }}, V s^{\text {label }}, \rho^{\text {label }}\right) \mid \rho^{\text {low }}\right)-\rho^{\text {label }}\right|\right] \\ & L_{\text {close }}^5=\frac{1}{M} \sum_i^M\left[\mid F\left(G\left(S^* \mid V p^{\text {low* }}\right), G\left(S^* \mid V s^{\text {low* }}\right)\right. \text {, }\right. \\ & \left.\left.G\left(S^* \mid \rho^{\text {low* }}\right)\right)-S^* \mid\right] \\ & \end{align}$$

故综上，最终的生成器损失函数为

$$L_{I,L} = L^g+\beta(L^1_{open}+L^2_{open})+\alpha(L^1_{close}+L^2_{close}+L^3_{close}+L^4_{close}+L^5_{close})$$

其中$\alpha,\beta(\beta \gg \alpha)$为约束系数，分别控制开环和闭环部分的贡献。

训练流程

• 首先将带标签数据组作为输入训练判别器
• 训练G和F

带标签数据由精确Zoeppritz方程得到

在一个训练epoch内，判别器训练两次，G和F训练一次。成为对抗训练

训练超参数设定

• 约束系数分别为$\lambda = 10, \alpha = 50, \beta = 1500$
• epoch = 300, batchsize = 34, 学习率=10exp-4, 衰减率为0.99

评价标准

为了量化反演结果的准确性，我们计算了每个道的皮尔逊相关系数( PCC )以及反演结果与真实模型之间的mse。两者均定义

$$\begin{aligned} & PCC(x,y)=\frac{Cov(x,y)}{\sqrt{Var(x)\sqrt{Var(y)}}}\\ & mse(x,y) = \frac{1}{M \times N}\sum^M_i\sum^N_j(x_{i,j}-y_{i,j})^2 \end{aligned}$$

本文方法的反演结果与其他两种方法相比具有更高更紧凑的PCC和更低的mse

我们还采用Frechet起始距离( FID )评分来评估反演结果。它能比inception score( IS )更好地捕捉生成结果与真实结果的相似性.当FID评分越低时，预测结果越接近真实模型。

$$\mathbf{FID}(x,y)=||\mu_x-\mu_y||^2_2+\mathbf{Tr}\left(\sum_x+\sum_y-2\left(\sum_x\sum_y\right)^{\frac{1}{2}}\right)$$

其中x和y分别为预测结果和真实模型，$\mu$为平均值。$\sum$为特征向量的协方差矩阵。$\mathbf{Tr}$为矩阵的迹

创新点： - 损失函数使用Wasserstein距离代替交叉熵。 - 利用弹性参数的低频信息作为条件输入缓解横向不连续性。 - 使用平均绝对误差( MAE )代替均方误差( mse )作为损失函数来提高网络训练的鲁棒性

结论

CMcWGAN利用弹性参数的低频信息作为条件输入缓解了横向不连续问题，提高了反演结果的精度。利用合成地震角道集的实验结果表明，CMcWGAN比cGAN具有更好的横向连续性，比传统的贝叶斯AVO反演方法具有更高的反演精度。在标签不足的情况下，CMcWGAN能够实现高精度的AVO反演，并且对含噪角度道集具有鲁棒性。