Directional Total Variation Regularized High-Resolution Prestack AVA Inversion

方向全变差正则化高分辨率叠前AVA反演

摘要

当前地震反演算法存在空间模糊和低分辨的问题，全变分(TV)正则化通过突出一阶差分的稀疏性来保留数据的空间变化边界，当数据不沿空间网格方向变化时，TV正则化容易产生阶梯效应。

该方法包括三个基本步骤:

• 从地震数据中估计地震斜率属性
• 将地震斜率属性引入TV正则化以建立目标函数
• 通过split-Bregman算法对目标函数进行优化。

对比表明，该方法能够较好地揭示地下模型的细节，有效地缓解了阶梯效应和伪影，进一步提高了反演结果质量

引言

地震数据中的走时信息通常对应于长波长分量，往往与构造信息有关，而振幅和波形信息通常对应于中短波长分量，往往与岩性信息有关。目前叠前AVA反演主要关注振幅信息，而与构造信息相关的长波长成分关注不够。所以本文提出了地震斜坡属性，利用平面波破坏( PWD )技术可以提取地震斜坡属性，其是与地震长波长分量相关的地震属性之一。它也是一种很好的横向约束条件，得到了广泛的应用。

Plane-wave destruction

参考论文"Applications of plane-wave destruction filters"

平面波破坏滤波器源于用于表征地震数据的局部平面波模型。这些滤波器可以被认为是频率-距离( F-X )预测误差滤波器的时间-距离( T - X)类似物和T - X预测误差滤波器的替代。滤波器是借助于局部平面波方程的隐式有限差分格式构造的。

平面波破坏滤波器由克拉尔布特( 1992 )提出，通过局部平面波的叠加来表征地震图像。它们被构造为平面波微分方程的有限差分模板。在许多情况下，局部平面波模型是地震数据的一种非常方便的表示。(滤波器的设计是为了破坏局部平面波。然而在数据插值等应用中，它们往往被用来重建局域波的缺失部分)

根据局域平面波的物理模型，我们可以将PWD滤波器的数学基础定义为局域平面微分方程

$$\frac{\partial P(x,t)}{\partial x} + \sigma(x,t) \frac{\partial P(x,t)}{\partial t}=0$$

其中$\sigma$表示地震斜率。进行傅里叶变换得到

$$\frac{d \hat{P}}{dx} + i\omega\sigma\hat{P} = 0$$

其中$\hat{P}$表示P的傅里叶变换

通过微分方程的求解（即方程左右同时乘$e^{i\omega\sigma x}$左式化为$(e^{i\omega\sigma x} \hat{P})'$），可得到通解为

$$\hat{P}(x) = \hat{P}(0)e^{i\omega\sigma x}$$

进行Z变换得到

$$\hat{P}_{x+1}(Z_t) = \hat{P}_{x}(Z_t)\frac{B(Z_t)}{B(1/Z_t)}$$

其中$\frac{B(Z_t)}{B(1/Z_t)}$表示全通滤波器，因为其零点与极点成对出现，所以只改变信号幅度，用于逼近$e^{i\omega\sigma}$

将上式转为二维，可得

$$\hat P(Z_t,Z_x) - \hat P(Z_t,Z_{x-1})\frac{B(Z_t)}{B(1/Z_t)} = 0$$

预测误差滤波器为

$$A(Z_t,Z_x) = 1 - Z_x\frac{B(Z_t)}{B(1/Z_t)}$$

本文使用上式滤波器的改进版

$$C(Z_t,Z_x) = A(Z_t,Z_x)B(1/Z_t) = B(1/Z_t) - Z_xB(Z_t)$$

通过求解$C(Z_t,Z_x)P(Z_t,Z_x) = 0$即可进行求解地震斜率属性

在地震数据中，优化函数为

$$C(\sigma)d=0$$

其中d为观测数据，通过高斯牛顿等优化策略得到$\sigma$，即地震斜率属性。

纹理由一个随机数场与平面波的逆进行卷积得到，利用螺旋滤波技术(克拉尔布特, 1998; Fomel, 2000)构造逆。

反问题构造

根据贝叶斯理论，目标函数可以表示为

$$J(m) = ||d-Gm||^2_2+\lambda Rc(m)$$

其中Rc(m)表示先验分布，这样的假设可能导致结果过于平滑。这样的反演结果对储层内部细节和储层边界的刻画能力较差。所以提出了TV正则化

TV正则化目标函数

$$J_{TV}(m) = J(m)+\alpha(||\nabla_x m||_1+||\nabla_y m||_1)$$

DTV正则化

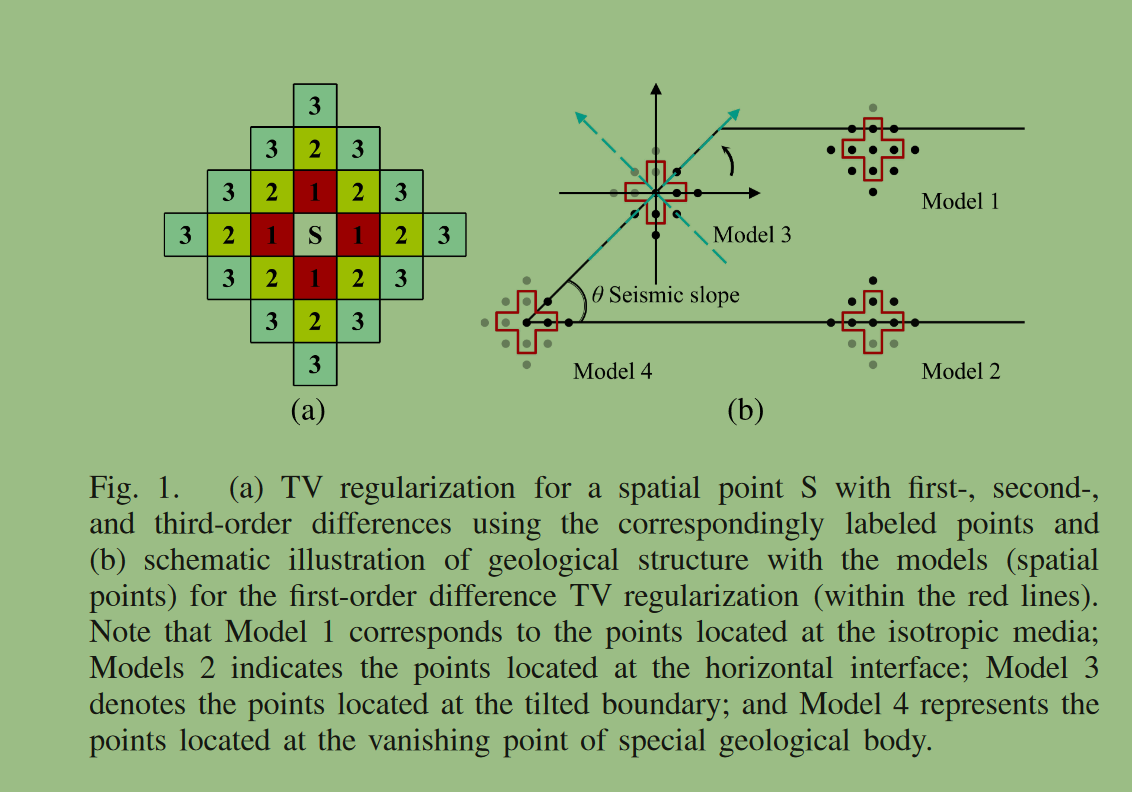
(a)对具有一阶、二阶和三阶差分的空间点S。( b )显示了断层处的地层，我们将这四个位置点作为模型1 - 4对应的模型。红色方框表示参与一阶差分运算的点。模型1表示地层内部的点，使用传统的反演算法可以得到很好的结果。模型2表示位于水平地层分界面的点。为了清晰地刻画出此时的信息，采用传统的TV正则化可以得到效果理想的结果。模型3对应倾斜断层处的点，在使用TV正则化时不能很好地描述断层界面。由于TV不适合局部结构具有优势方向，因此在模型4中也会出现同样的情况，对应地层消亡带的点。DTV正则化引入地震倾角属性，将数据从笛卡尔坐标系投影到沿和垂直于地震倾角的方向，蓝色虚线箭头表示DTV正则化。

$$J_{DTV}(m) = J(m)+\alpha(||\nabla_1 m||_1+||\nabla_2 m||_1)$$

其中$\nabla_1$和$\nabla_2$分别表示沿和垂直于地震倾角主方向的梯度算子,在得到地震斜率属性后可通过尺度矩阵和旋转矩阵得到这两个算子

$$\left(\begin{matrix} \nabla_1 \\ \nabla_2 \end{matrix}\right)= \left(\begin{matrix} a_1 \quad 0\\ 0 \quad a_2 \end{matrix}\right) \left(\begin{matrix} \cos\theta \quad -\sin\theta \\ \sin\theta \quad \cos\theta \end{matrix}\right)\left(\begin{matrix} \nabla_x \\ \nabla_y \end{matrix}\right)$$