数学基础

泰勒展开

一元

$$f(x)=f(x_0)+f^{'}(x_0)(x-x_0)+\frac{f^{''}(x_0)}{2!}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x)\tag1$$

多元

$$f(x,y)=f(x_k,y_k)+\left[ \begin{matrix}f'_x(x_k,y_k)&f'_y(x_k,y_k)\end{matrix} \right]\left[\begin{matrix}x-x_k\\y-y_k\end{matrix} \right]+\\\frac1{2!}\left[ \begin{matrix}x-x_k&y-y_k\end{matrix} \right]\left[ \begin{matrix}f''_{xx}(x_k,y_k)&f''_{xy}(x_k,y_k)\\ f''_{yx}(x_k,y_k)&f''_{yy}(x_k,y_k)\end{matrix} \right]\left[\begin{matrix}x-x_k\\y-y_k\end{matrix} \right]+\cdot\cdot\cdot+o^n\tag2$$

和差化积

正加正，正在前；余加余，余并肩；正减正，余在前；余减余，负正弦；

$$\left\{\begin{matrix} \sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\\ \sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\\ \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\\ \cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}\\ \end{matrix}\right.$$

斯涅尔定律

$$p = \frac{\sin \theta_1}{\alpha_1} = \frac{\sin \theta_2}{\alpha_2}=\frac{\sin\varphi_1}{\beta_1}$$

其中$\theta$为入射/传播角，$\alpha$为p波在介质中的相速度，$\varphi$为S波反射/传播角，$\beta$为S波速度

矩阵范数

诱导p-范数

$$||A||_p=\max_{x\neq 0}\frac{||Ax||_p}{||x||_p}=\max_{x\neq 0}\frac{\left(\sum_{i=1}^m|\sum_{j=1}^n a_{ij}x_{j}|^p\right)^{1/p}}{\left(\sum_{j=1}^n|x_j|^p\right)^{1/p}}$$

$$||A||_1=\max_{1\leq j\leq n\sum}\sum^m_{j=1}|a_{ij}|$$

$$||A||_\infty=\max_{1\leq i\leq m\sum}\sum^n_{i=1}|a_{ij}|$$

$$||A||_2=\sqrt{\lambda_{\max}{A^*A}}$$

当p = 2（欧几里德范数）时，诱导的矩阵范数就是谱范数。矩阵A的谱范数是A最大的奇异值或半正定矩阵$A^*A$的最大特征值的平方根

元范数

$$||A||_p=\left(\sum^m_{i=i}\sum^n_{j=1}|a_{ij}|^p\right)^{1/p}$$

Schatten范数

用矩阵的奇异值定义的范数

$$||A||_p=\left(\sum^{\min\{m,n\}}_{i=1}\sigma^p_i\right)^{1/p}$$

变分法与欧拉-拉格朗日方程

参考：

浅谈变分原理

假设我们有两个定点$(a,p)$和$(b,q)$，连接这两点的任意曲线的方程 $y = y(x)$ 都将满足如下的边界条件：

$$y(a)=p, \quad y(b)=q$$

现在考虑如下形式的定积分：

$$I = \int_a^b f(y,y')\mathrm{d}x$$

我们期望找到一个具体的$y(x)$,使得$I$有极值（极大或极小）

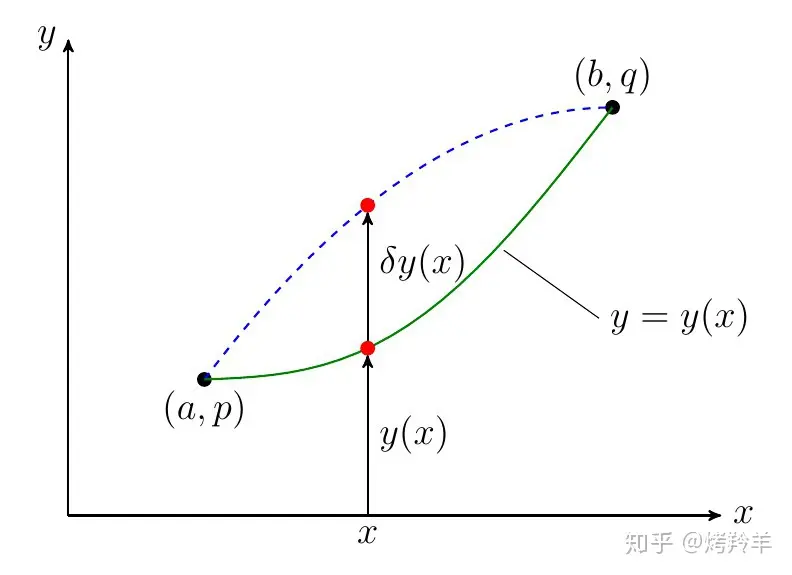
Euler-Lagrange Equation

如果$I$有极值，对任意满足边界条件的 $\delta y(x)$ 都必须有$\delta I = 0$，这就要求：

$$\frac{\partial f}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{\partial f}{\partial y'} \right) = 0$$

梯度向量

$$\nabla f = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix} \\ $$

雅可比矩阵

$${\displaystyle \mathbf {J} ={\begin{bmatrix}{\dfrac {\partial \mathbf {f} }{\partial x_{1}}}&\cdots &{\dfrac {\partial \mathbf {f} }{\partial x_{n}}}\end{bmatrix}}={\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{1}}{\partial x_{n}}}\\\vdots &\ddots &\vdots \\{\dfrac {\partial f_{m}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{m}}{\partial x_{n}}}\end{bmatrix}}} \\ $$

矩阵求导是线性代数和微积分的交叉领域，它在机器学习、深度学习、优化等领域中都有广泛的应用。下面是矩阵求导的一些性质和技巧：

• 线性性：矩阵求导具有线性性。即对于矩阵 $A$ 和 $B$，以及常数 $\alpha$，有 $\frac{\partial (\alpha A + B)}{\partial x} = \alpha\frac{\partial A}{\partial x} + \frac{\partial B}{\partial x}$。

• 乘法规则：矩阵求导的乘法规则与标量求导的乘法规则相似，即对于矩阵 $A$ 和 $B$，有 $\frac{\partial AB}{\partial x} = \frac{\partial A}{\partial x}B + A\frac{\partial B}{\partial x}$。

• 转置规则：对于矩阵 $A$，有 $\frac{\partial A^T}{\partial x} = (\frac{\partial A}{\partial x})^T$。

• 迹运算规则：对于矩阵 $A$，有 $\frac{\partial \text{tr}(A)}{\partial x} = \text{tr}(\frac{\partial A}{\partial x})$。

• 逆运算规则：对于矩阵 $A$ 和 $B$，有 $\frac{\partial A^{-1}}{\partial x} = -A^{-1}\frac{\partial A}{\partial x}A^{-1}$，以及 $\frac{\partial (A^{-1}B)}{\partial x} = -A^{-1}\frac{\partial A}{\partial x}A^{-1}B + A^{-1}\frac{\partial B}{\partial x}$。

• 对数运算规则：对于矩阵 $A$，有 $\frac{\partial \log(\det(A))}{\partial x} = \text{tr}(A^{-1}\frac{\partial A}{\partial x})$。

• Hadamard积规则：对于矩阵 $A$ 和 $B$，有 $\frac{\partial (A\odot B)}{\partial x} = \frac{\partial A}{\partial x}\odot B + A\odot \frac{\partial B}{\partial x}$，其中 $\odot$ 表示Hadamard积。

对于形如 $xA=b$ 的线性方程组，我们可以使用矩阵分解或者迭代算法来求解。下面介绍两种常用的方法。

QR 分解法

QR 分解法是一种求解线性方程组的常用方法，它可以将系数矩阵 $A$ 分解为正交矩阵 $Q$ 和上三角矩阵 $R$ 的乘积，即 $A=QR$。然后将方程组 $Ax=b$ 变形为 $QRx=b$，令 $y=Q^Tb$，则原方程组变为 $Rx=y$，可以通过回代法求解。具体来说，可以先求解 $y=Q^Tb$，然后从最后一行开始，依次求解 $x_i=\frac{1}{r_{ii}}(y_i-\sum_{j=i+1}^n r_{ij}x_j)$，直到求解出 $x_1$。

共轭梯度法

共轭梯度法是一种迭代算法，用于解决对称正定线性方程组 $Ax=b$，其中 $A$ 是对称正定矩阵。对于形如 $xA=b$ 的方程组，我们可以对其进行变形，得到 $A=x^Tx$ 和 $b=x^Tb$，然后再使用共轭梯度法求解。具体来说，可以按照共轭梯度法的步骤进行迭代，只需要在每次迭代时，将搜索方向和残差都乘以 $x^T$ 即可。

总之，对于形如 $xA=b$ 的线性方程组，可以使用 QR 分解法或者共轭梯度法进行求解。QR 分解法适用于一般的线性方程组，而共轭梯度法适用于对称正定线性方程组，且具有更快的收敛速度。

参考网址

深度学习中的矩阵求导入门

矩阵的四大基本空间