地震信号反演¶

参考： https://www.geoexpro.com/articles/2013/08/geophysics-a-simple-guide-to-seismic-inversion

反演的概念¶

正演通过已知的地质模型来得到参数
反演通过测量到的数值来估计实际模型，基于声波测量的反演，经常用作校准岩石属性。

反演(Seismic inversion)¶

即通过测量的反射数据得到岩石的属性（称为阻抗，声速和体积密度的乘积）强振幅与岩石边界有关，在反向数据集中，振幅代表岩石内部性质。

确定性反演(Deterministic Inversion)¶

将缺失的低频信号引入反演，从而得到趋势。但是低频这一部分只是简单建模并加入相对阻抗中。注意有可能这个趋势不是由于地震反射波引起的，而是平滑的模型带来的，所以要注意解释的是地震数据，而不是模型。 deterministic inversion = relative inversion + model

联合反演(Simultaneous Inversion)¶

地震数据包含有关地球岩石性质的附加信息，可以使用几种不同的方法对这些信息进行反演。它利用pre-stack gather(或该数据的部分叠加，如角度叠加)同时反演多个岩石属性参数。也是一种确定性反演，所以也要注意上面的问题。最后通过高通滤波把模型滤掉更安全。

EEI(Extended Elastic impedance) Inversion¶

反演前执行某种类型的校准，使用特殊角度项 $\chi$ ，它的投影范围从-90° 到 +90°。可为数据找到两个特征角，最大振幅代表岩体立方，最小振幅代表流体立方

随机反演(Stochastic Inversion)¶

它消除了调谐效应，对不确定性建模，可以在细尺度上进行计算;但是有更高的成本和大量数据。

建模¶

调谐问题¶

反演振幅不仅与岩石性质有关，还与地层厚度有关。如果厚度接近特定地震的“调谐”频率，那么振幅可能会比实际情况明显，可能导致地层厚度的变化被误解为岩石性质的变化，所以要进行去除调谐效应。

分辨率不一致问题¶

模型和地震阻抗之间在垂直分辨率上的巨大差异，模型分辨率高，会产生误导性的流体流动特征。

错误的趋势问题¶

之前确定性反演有提到，可能会产生遵循模型的错误趋势，因此要将模型去除。

相关概念¶

相对阻抗(relative impedance)¶

是直接从没有模型输入的地震数据中估计出来的，是一种鲁棒的地震特性。数据不记录低频，故无趋势

彩色反演(colored inversion)

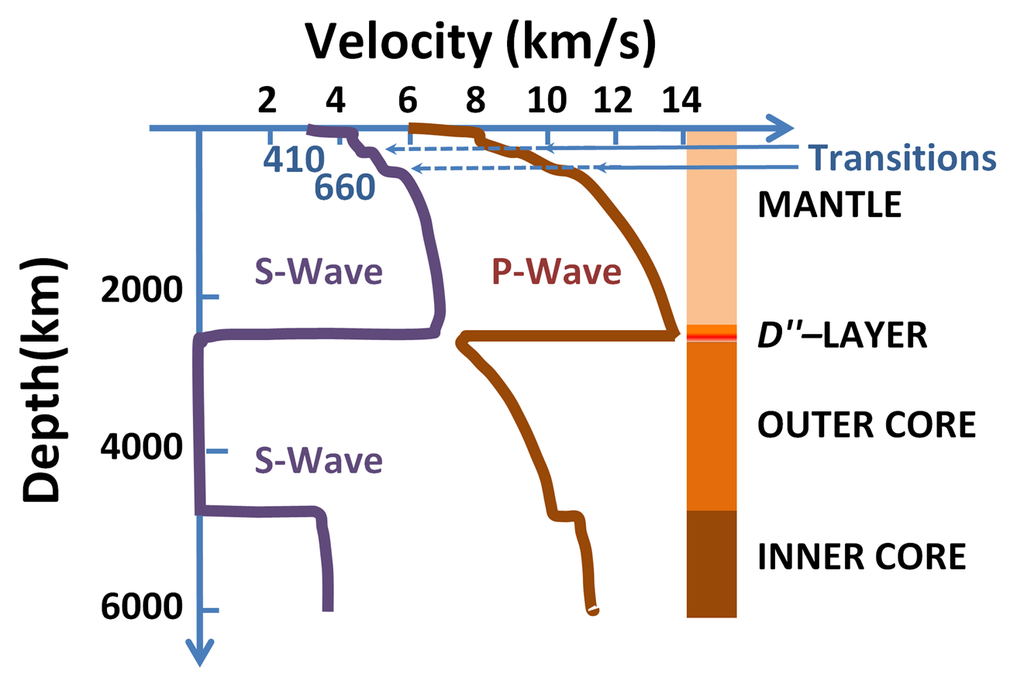
p wave¶

primary or pressure wave 主波

参考：https://en.wikipedia.org/wiki/P_wave

平行于波传播方向的质点运动传播(声波)，传播速度比其他地震波快，当它们通过半固态地幔和液态外核之间的过渡时，会发生轻微的折射。因此，在距离震源103°到142°之间有一个P波“阴影区”，无法记录。

速度计算：

$v_p=\sqrt{\frac{K+\frac{4}{3}\mu}{\rho}}=\sqrt{\frac{\lambda+2\mu}{\rho}}=\sqrt{\frac{M}{\rho}}$

由于密度变化很小，所以主要由 $K和\mu$ 决定

s wave¶

secondary or shear wave 次波

参考：https://en.wikipedia.org/wiki/S_wave

垂直于波传播方向的质点运动传播,p波在非正入射时撞击界面会产生s波,波速仅次于P波，S波无法穿越外地核，因为流体不支持剪切，所以S波的阴影区正对着地震的震源。

粒子运动与传播方向在垂直面内为SV-wave,粒子运动与传播方向在水平面进行为SH-wave

以上两种阻抗可通过结合得到另外两种属性, $\lambda\rho$ 与 $\mu\rho$ p波阻抗(IP)和 $\lambda\rho$ 性质告诉我们孔隙空间的影响，如孔隙度和碳氢化合物(存在或饱和度)。s波阻抗(SI)和μρ可以在去除孔隙空间和流体的影响后，为我们提供有关岩性的信息。通过比较每种产出类型之间的岩石性质异常，就有可能更好地了解异常是否可能是由孔隙度/饱和度变化或岩性变化引起的。

三项反演：得到IP，SP,体密度（sonic,shear,bulk density),体密度很难得到，对地震幅度影响很小且只存在于大角度情况下(>40°)

反射系数¶

表示反射波与入射波的振幅比，该参数决定垂直入射的地震波反射后的振幅变化，其大小与界面两侧声阻抗不同的地层的密度和速度相关。这样反射系数也表示为界面两侧地层声阻抗差与声阻抗和的比值。

合成地震道¶

将地震脉冲信号合并到时间域模型上得到合成地震道。该过程在数学上称为褶积。地震脉冲信号或子波，表示来自某个震源的能量包。选择一个模型子波来匹配处理后的地震数据的振幅、相位和频率特征值。将该子波与反射系数模型进行褶积产生合成地震道，该地震道表示被模拟地层对输入地震脉冲信号的响应。如果模拟道上有噪音干扰、信号衰减及多次反射现象，还需要进行其他处理。

子波¶

参考: 褶积与反褶积是什么?

可以认为是地震波的初始能量，地震波传播的过程就是这个子波通过地下介质的过程。

叠加¶

是一种通过平均很多地震道达到信号加强目的的技术，参与平均处理的地震道代表着共反射中心点的不同偏移距集合的地震记录。产生的叠加道被认为是共中心点CMP上垂直入射的反射响应。地震道叠加能够加强信号，降低噪音。

叠加道¶

因大偏移距地震波传播距离较远，需要对每一个道集进行时间校正，即正常时差校正（NMO），拉平大偏移距到达波；将拉平后的地震道取平均值得到一条叠加道，该道代表垂直入射（零偏移距）地震道。

叠后反演¶

假设反射层上覆介质速度呈渐进变化，并且叠加道平均振幅与垂直入射道振幅相等，那么叠加就是相当合理的处理步骤。多数情况下，以上假设条件都能成立，这样就可以在叠加后的数据上进行反演。将叠加道同合成道（反射系数模型和子波褶积后合成的地震道）进行对比，并用这两种道的误差修正反射系数模型，使合成道的下一次迭代更逼近叠加道。重复以上过程，直到合成道和叠加道达到最佳拟合。

叠前反演¶

当地震道振幅随偏移距变化较为剧烈时，叠加不再适合，这样就只能在未叠加道上进行反演

加权叠加：在叠加前对数据样本使用时间和偏移量变化的权重。

共中心点(CMP)¶

Common Midpoint

地震资料采集中，若地下界面为水平界面，则共反射点在地面的投影必为炮集中拥有共反射点接受距的中心点，因此称为共中心点。把不同炮集中拥有共中心点的道抽取出来，形成一个新的集合，称之为共中心点道集——CMP道集。在多道地震采集中，地表上位于震源和接收器中间的点，由多个震源-接收器对共用。公中心点垂直于共深度点或共反射点之上。

共深度点(CDP)¶

Common Depth Point

在多道地震采集中，当地层不下沉时，反射面深度处的共反射点，或波从震源传播到反射面再到接收器时的中间点。在平面层的情况下，共深度点垂直低于共中心点。在倾斜层中，多个源和接收点没有共深度点，因此需要对倾斜偏移进行处理，以减少数据的错误或不适当的混合。

共反射点(CRP)¶

Common Refledtion Point

在多道地震采集中，反射面上的共同中点，或波从震源到反射面再到接收器时的中点，如果反射面是水平的，则该中点由多个位置共享。与公深度点一样，但在倾斜层中，共反射点不存在。

L1&L2 Regularization¶

从数学上来讲，就是在损失函数中加个正则项（Regularization Term），来防止参数拟合得过好。

参考链接：https://www.zhihu.com/question/26485586/answer/91420865

L1-Regularization $$\lambda \sum_{i=0}^k|w_i| $$
L2-Regularization $<span class="arithmatex"><span class="MathJax_Preview">\lambda \sum_{i=0}^kw_i^2</span><script type="math/tex">\lambda \sum_{i=0}^kw_i^2$

AVO(amplitude variation with offset)¶

Ostrander首次提出 地震道振幅随偏移距变化，此时叠加道振幅不等于垂直入射道（即零偏移距道）的振幅，偏移距大小与入射角有关

参考文章：Tutorial: AVO inversion

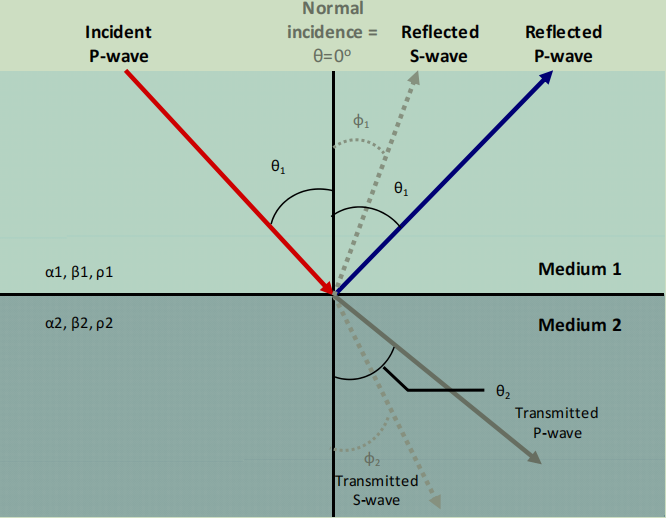
准备步骤与地震道叠加相同，首先将共中心点道组合成道集，并按偏移距进行排序，然后用正常时差速度模型对到达波进行拉平处理，拉平过程中注意保护振幅。得到的叠加道并不与零偏移距道相似；换句话说，叠加处理并不能保护振幅。偏移距与入射角的关系取决于射线路径。多数 AVO 反演算法基于反射振幅与入射角之间的关系。因此，反演前的附加处理步骤就包括将偏移距转换成入射角，

部分叠加方法：将每一个CMP集内的近偏移距道进行叠加，再将所有叠加道组成近偏移距道集。采用同样的方法建立中偏移距道集和远偏移距道集，然后对每种偏移距道集进行分别反演。可能会导致某些AVO信息丢失

Zoepptriz equation¶

描述平面波入射射线和离散振幅之间关系，但由于地下大量未知与地球的复杂性，应用在地震数据中有很大困难，所以提出了很多近似方法

声阻抗反演¶

第一个公式基于连续的地球模型，其中弹性参数随深度连续变化, 模型的离散化得到反射率函数的第j分量为

$r[j] = \frac{1}{2}\log\frac{z[j+1]}{z[j]}$

第二个公式是由一个分层大地模型导出的，其中第j层的反射系数表示为

其中 $z[j] = \rho[j] v_p[j]$

反演问题¶

${d = Lm}$

m: model, d: recorded data, L: forward-modeling operator

性质： - 有解，由于噪声会导致方程过度确定或不不一致导致无解：残差加权和，惩罚函数 - 唯一解：正则化 - 解持续依赖于数据：正则化

traveltime tomography - 1. 离散化模型m，每个网格对应slowness Nx1 - 2. 离散化数据d Mx1 - 3. 离散化运算符L MxN

故：

$\displaystyle\sum_{j}l_{ij}m_j=d_i\tag {1.1}$

1. 线性化：由于L取决于m 令 $m^{(0)}=m_o$ ( $m_o$ 指预测值), 使其接近真实模型并线性化数据与模型之间的关系进行迭代收敛

利用泰勒展开式

( $d_i随着\pmb m变化， \pmb m 为真实模型，\pmb m_o为预测值$ )

$d_i(\pmb m)\approx d_i(\pmb m_o) + \displaystyle\sum_j\left.\left[\frac{\partial {d_i(\pmb m)}}{\partial m_j}\right]\right|_{m_o}\delta m_j\tag{1.2}$

化简得

$\delta\pmb d(\pmb m) = \pmb L\delta\pmb m\tag{1.3}$

$l_{ij}=\frac{\partial d_i(\pmb m_o)}{\partial m_j} 代表第i个数据对模型第j个cell的扰动$

疑问1¶

$\displaystyle\sum_j\left.\left[\frac{\partial {d_i(\pmb m)}}{\partial m_j}\right]\right|_{m_o}\delta m_j 与 \left.\left[\frac{\partial {d_i(\pmb m)}}{\partial \pmb m}\right]\right|_{m_o}\delta\pmb m 相等吗？$

1. 正则化不稳定解问题规定一个最小化目标函数：（数据残差的p范数与惩罚条件）

$\epsilon = \frac{1}{p}\parallel\pmb L\delta\pmb m-\delta\pmb d\parallel^p_p+\eta^2g(\pmb m)\tag{1.4}$

当p=2时,即二范数得

$\delta\pmb m=\left[\pmb {L^TL}+\eta^2\pmb I\right]^{-1}\pmb{L^T}\delta\pmb d\tag{1.5}$

疑问2（怎么推导⬆）¶

1. 迭代化正则(具体见p30) 为了减小计算量

$\left[\pmb{L^TL}\right]_{ij}\approx\left[\pmb{L^TL}\right]_{ii}\delta_{ij}$

规定正则化与步长参数 $\alpha$