数据结构

数据结构 C++版

由于科研课业压力较大,没时间更新这部分内容,寒假一定补齐

二叉树

c++实现二叉树

数据结构二叉树(C++)

//构造
//树的结点的结构体定义
class Tree {
    int val;
    Tree* left;
    Tree* right;
};

先序遍历: 根->左->右

//递归
void preorder(Tree* root, vector<int> res)
{
    if(root==nullptr)
    {
        return;
    }
    res.push_back(root);
    preorder(root->left);
    preorder(root->right);
}

堆

堆是一颗完全二叉树,节点坐标为i时,左下节点坐标为2*i+1, 右下坐标为2*i+2

根据堆序性可以将其分为大根堆和小根堆两种,大根堆即根节点大于其子节点,小根堆即根节点小于其子节点

有上滤和下滤两种操作,复杂度均为O(logN)

插入元素时 插到堆尾部,不断与父节点比较,如果大于父节点就上移,直到满足堆序性,这样的操作就称为上滤,也可以插到堆顶,不断与子节点比较,如果小于就下移,直到满足堆序性,这样的操作称为下滤

建堆,分为自顶向下(尾部插入上滤)和自下向上(从倒数第二排开始下滤)

小根堆实现优先队列

队列每次弹出最小元素,可以用小根堆弹出根节点实现,之后再对堆进行排序即可,复杂度O(logN),所以如果依次弹出队列,将会得到一个有序的数组,这也就是堆排序,但考虑到空间复杂度,希望不开辟额外的空间,可以使用大根堆排序

每次将根节点与最后一个节点交换,之后重新构建堆,如此往复,会得到层序遍历为正序的小根堆

//自定义比较函数的大根堆
struct Comp
{
    bool operator()(Point* a, Point* b)
    {
        return a->val>b->val;
    }
}
priority_queue<Point*, vector<Point*>, Comp> q;

并查集

算法学习笔记(1) : 并查集

求连通域大法

class UnionFind{
private:
    vector<int> f;//f[i]表示节点i的祖宗节点索引
    vector<int> rank;//rank[i]表示节点i所在的树深度
public:
    UnionFind(int n)//初始化n个节点,n为索引,此时还没有联通
    {
        f.resize(n, 0);
        iota(f.begin(), f.end(), 0);//每个节点的f都为自身
        rank.assgin(n, 1);//每个节点的rank(也就是深度)为1
    }
    int find(int i)//查找i的祖宗节点
    {
        //简写版
        return i==f[i]? i : f[i]=find(f[i]);
        // 详解版
        // if(i==f[i])//如果节点的f为自己, 就返回自己
        // {
        //     return i;
        // }
        // else
        // {
        //     f[i] = find(f[i]); // 将f[i]赋为祖宗节点(路径压缩)
        //     return f[i];
        // }
    }
    void merge(int i, int j)//合并两个连通域
    {
        //找出这两个点的祖宗节点,只对祖宗节点进行合并
        int x = f[i];
        int y = f[j];
        if(x==y)
            return;
        //按照rank路径压缩, 深度小的树合并为深度高的树的子树
        if(rank[x]>rank[y])
        {
            swap(x,y);
        }
        f[x] = y;
        //如果两颗树深度一样,就要让rank+1
        if(rank[x]==rank[y])
            rank[y]++;
    }
}

关键在于如何merge, 思路很重要,

• 721题账户合并要将所有邮箱一样的合并到一起,遍历数组,怎么判断这个邮箱是否有一样的? 自然想到使用哈希表,存邮箱与索引的映射,这样在遍历的时候如果遇到邮箱在哈希表里,就merge, 如果不在,就插入
• 947题要将同列同行的元素合并, 比如a和b同行,b和c同列, a与c不同行不同列, 这种情况也是连通域,遍历矩阵,怎么判断当前元素之前同行或者同列的元素?行号列号自带索引信息,所以可以将行列索引信息用一维数组表示, 遍历时merge当前元素的行和列

题单

• 721. 账户合并
• 947. 移除最多的同行或同列石头

线段树

单调栈

顾名思义，元素呈一种顺序排列的栈，满足先进后出

下面为找到以raw[0]为第一个元素的递减单调栈

stack<int> container;
vector<int> raw = {21,3,4,61,2,5,32,1};
for(int i = 0; i<raw.size(); i++)
{
    while(!container.empty()&&container.top()>raw[i])
    {
        container.pop();
    }
    container.push(raw[i]);
}

题单

树状数组

带你发明树状数组！附数学证明（Python/Java/C++/Go/JS/Rust）

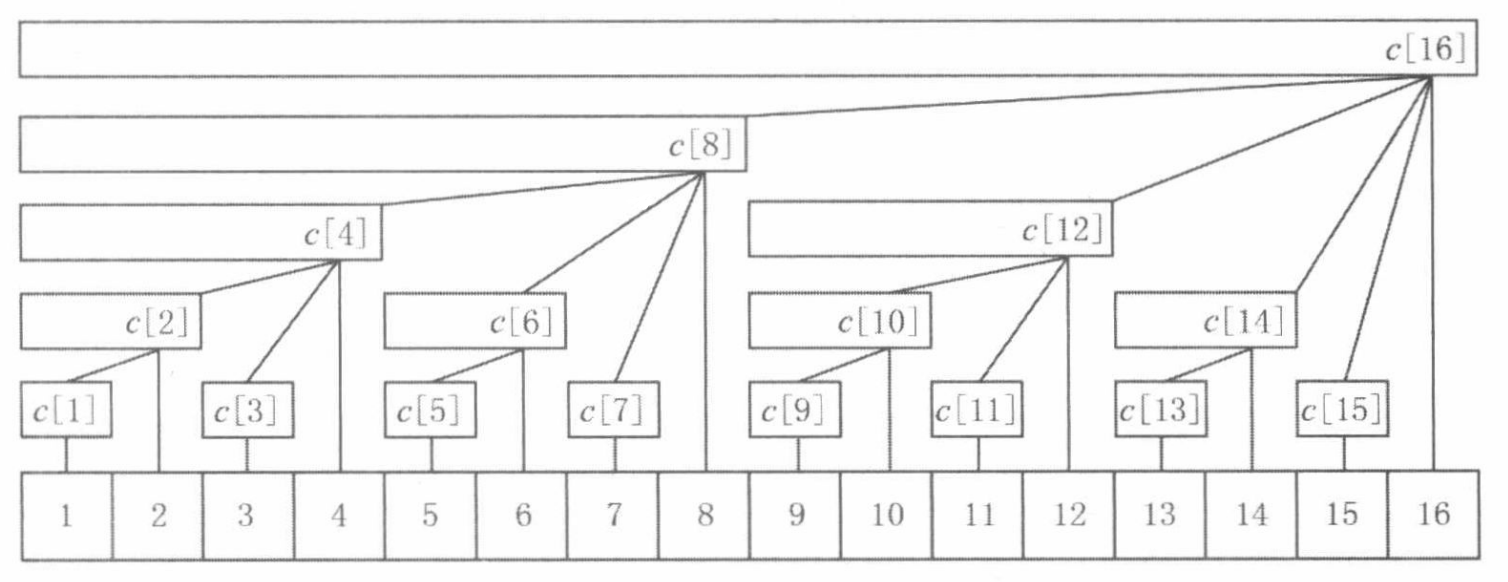
模板

//树状数组模板，用树状数组存第[i]个数存关键区间的值
//get可求得[1,i]的区间和，累减lowbit，然后相加
//i涉及到二进制位运算，从1开始而不是0，所以大小为n+1
class BinaryIndexedTree
{
private:
    vector<int> t;
public：
    BinaryIndexedTree(int n) : t(n+1) //t[0]无意义，始终为0，索引从1开始，故长度要加1
    void add(int i)//i位置的元素加1
    {
        while(i<t.size())
        {
            t[i]++;
            i += i&-i; //取lowbit，i二进制数中最低一位的值，不断累加就是i改变所影响的其他元素
        }
    }
    int get(int i)//计算[1,i]和区间和
    {
        int sum = 0;//等于0时说明已经加完了，跳出循环
        while(i>0)
        {
            sum+=t[i];
            i -= i&-i; //等价于i &= i-1， 不断累减其lowbit, 相加就是[1,i]的区间和
        }
    }
}

前缀树Trie

多叉树，26叉树, 存储前缀,字符串,且具有唯一性

class Trie{
private:
    bool is_end;
    Trie* next[26];//数组的26个元素(一般指代26个字母)是指针,指向Trie
public:
    Trie()
    {
        is_end = false;
        // memset(next, 0, sizeof(next));
    }
    void add(string s)//插入字符串
    {
        Trie* t = this;
        for(auto c: s)
        {
            if(t->next[c-'a']==nullptr)
            {
                t->next[c-'a'] = new Trie();
            }
            t = t->next[c='a'];
        }
        t->is_end = true;//代表是一个字符串而不是前缀
    }
    bool search(string s)
    {
        Trie* t = this;
        for(auto c: s)
        {
            if(t->next[c-'a']==nullptr)
                return false;
            t = t->next[c-'a'];
        }   
        return true;
    }

}

题单

• 周赛

位运算

分享｜从集合论到位运算，常见位运算技巧分类总结！

作者：灵茶山艾府 链接：https://leetcode.cn/circle/discuss/CaOJ45/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

特别地，只包含最小元素的子集，即二进制最低 1及其后面的 0，也叫 lowbit，s & -s 算出。举例说明：

     s = 101100
    ~s = 010011
(~s)+1 = 010100 // 根据补码的定义，这就是 -s  =>  s 的最低 1 左侧取反，右侧不变
s & -s = 000100 // lowbit

原码, 反码, 补码的基础概念

	正数	负数
原码	符号位为0，绝对值	符号位为1，绝对值
反码	本身	符号位不变，其余各个位取反
补码	本身	符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)