波在介质中的传播学习笔记
应变-能量密度和应力-应变关系
定义应变能是确定本构方程或应力-应变关系的第一步,它提供了描述物理介质静态和动态变形的基础。利用应力和应变张量的对称性,应变能体积密度的最一般形式是
2V=\sum_{I}^6\sum_{J\geq I}^6a_IJe_Ie_J
根据Voigt notation
e_I=e_{i(i)}=\partial_iu_{(i)},\quad I=1,2,3,\quad e_I=e_{ij}=\partial_ju_i+\partial_iu_j,\quad i\neq j\mathrm{~(}I=4,5,6)
其中u_i为位移分量, 应力由下式给出(矩阵形式右式)
\sigma_{ij}=\frac{\partial V}{\partial e_{ij}} \qquad or \qquad \sigma_{I}=\frac{\partial V}{\partial e_{I}}
利用笛卡尔符号和缩短符号,我们可以将各向异性弹性情况下的胡克定律写为
\sigma_{ij}=c_{ijkl}\epsilon_{kl}\qquad or \qquad \sigma_I = c_{IJ} e_J
使用矩阵表示法,上式应力-应变关系为
\sigma=\mathbf{C}\cdot\mathbf{e}
其中
\left.\mathbf{C}=\left(\begin{array}{cccccc}c_{11}&c_{12}&c_{13}&c_{14}&c_{15}&c_{16}\\c_{12}&c_{22}&c_{23}&c_{24}&c_{25}&c_{26}\\c_{13}&c_{23}&c_{33}&c_{34}&c_{35}&c_{36}\\c_{14}&c_{24}&c_{34}&c_{44}&c_{45}&c_{46}\\c_{15}&c_{25}&c_{35}&c_{45}&c_{55}&c_{56}\\c_{16}&c_{26}&c_{36}&c_{46}&c_{56}&c_{66}\end{array}\right.\right)
且主行列式大于零
在具有耗散的材料中,不能定义唯一的自由能密度函数(应变能), 在某些情况下,应变能是唯一的,例如具有基于指数松弛函数的内变量的粘弹性材料(Fabrizio和Morro, 1992,第61页)。当内部变量的数量小于物理(可观察)变量的数量时,唯一性保持
我们假设介质的性质不随时间变化(未老化的材料),并且,与无损情况一样,能量密度在应变场中是二次方的。我们引入本构方程作为应力和应变之间的卷积关系,假设等温条件。然而,如前所述,需要注意的是,应变能密度的形式并不是唯一的(参见拉博特诺夫, 1980 , p.72 )。与力学模型的类比为非弹性现象提供了一个相当普遍的描述。构建模块弹簧和阻尼器.在这些元素中,隐含着能量在弹簧中"储存",在阻尼器中"耗散"。这些元素的任意串联和并联提供了一个很好的唯象模型来描述许多材料的行为,从聚合物到岩石。克里斯滕森( 1982 , p . 86)、Hunter ( 1983 , p . 542)和Golden and Graham ( 1988 , p . 12 )定义了线性黏弹性情况(另见卡尔乔内, 1999a)中应变能的适当形式。
P65 等温、各向异性粘弹性介质的应力-应变关系为
\sigma_{ij}=\psi_{ijkl}*\partial_{t}\epsilon_{kl}
\psi_{ijkl}是松弛张量的分量, 矩阵表示为
\sigma=\Psi*\partial_{t}e,\quad(\sigma_{I}=\psi_{IJ}\partial_{t}e_{J}),
一般而言,在应力-应变关系由玻尔兹曼定律(Boltzmann law)给出的假设下,在没有精确定义应变-能量函数的情况下,只能说明在低频和高频极限下是一个对称矩阵
P197 时谐场用实部表示, 时间依赖性代入应力-应变关系得到(也就是傅里叶变换)
\sigma=\mathbf{P}\cdot\mathbf{e},\quad(\sigma_I=p_{IJ}e_J) \quad where\quad p_{IJ}=\int_{-\infty}^{\infty}\partial_{t}\psi_{IJ}(t)\exp(-\mathrm{i}\omega t)dt
P(x,\omega)为刚度矩阵, 对于非弹性介质,P的分量是复杂的和频率相关的。
请注意,Auld (1990a, p. 87)讨论的非弹性应力-应变关系是特殊情况。Auld引入了一个粘度矩阵η,使得P(ω) = C + iωη,其中C为低频极限弹性矩阵。该方程对应于Kelvin-Voigt应力-应变关系
cIJ表示弹性(或非松弛)刚度常数。则p_{IJ}(\omega \rightarrow \infin)=c_{IJ}。pIJ为复刚度。这些复刚度在弹性情况下等于真实的高频极限弹性常数cIJ。胡克定律可以用Voigt符号表示为
\left.\left(\begin{array}{c}\sigma_{11}\\\sigma_{22}\\\sigma_{33}\\\sigma_{23}\\\sigma_{13}\\\sigma_{12}\end{array}\right.\right)=\left(\begin{array}{cccccc}p_{11}&p_{12}&p_{13}&p_{14}&p_{15}&p_{16}\\p_{12}&p_{22}&p_{23}&p_{24}&p_{25}&p_{26}\\p_{13}&p_{23}&p_{33}&p_{34}&p_{35}&p_{36}\\p_{14}&p_{24}&p_{34}&p_{44}&p_{45}&p_{46}\\p_{15}&p_{25}&p_{35}&p_{45}&p_{55}&p_{56}\\p_{16}&p_{26}&p_{36}&p_{46}&p_{56}&p_{66}\end{array}\right)\cdot\left(\begin{array}{c}\epsilon_{11}\\\epsilon_{22}\\\epsilon_{33}\\2\epsilon_{13}\\2\epsilon_{12}\end{array}\right)
均匀入射波求解反射系数
假设入射波、反射波和透射波由上标I、R和T标识。
入射波质点速度为
v^{I}=\mathrm{i}\omega\exp[\mathrm{i}\omega(t-s_{1}x-s_{3}^{I}z)]
为了简单起见,水平慢度中的上标I在此处和之后的所有分析中都被省略了
对于均匀波,传播方向和衰减方向重合且s_{1}=\sin\theta/v_{c}(\theta),\quad s_{3}=\cos\theta/v_{c}(\theta)
传播方向与平面波前垂直。给定复慢度矢量的分量,则传播角和衰减角为
\tan\theta=\frac{\mathrm{Re}(s_1)}{\mathrm{Re}(s_3)}\quad\mathrm{and}\quad\tan\delta=\frac{\mathrm{Im}(s_1)}{\mathrm{Im}(s_3)}
由色散关系( 6.5 ),当p44 = p66 = ρv2c≡μ和p46 = 0时,我们得到
\mathbf{s}\cdot\mathbf{s}=s_{1}^{2}+s_{3}^{2}=\frac{1}{v_{c}^{2}}
式中:vc为复速度。复杂的慢度也可以表示为
\mathbf{s}=\mathbf{s}_{R}+\mathbf{i}\mathbf{s}_{I}=(s_{1},s_{3})^{\top}=(s_{1R}+\mathbf{i}s_{1I},s_{3R}+\mathbf{i}s_{3I})^{\top}
P233 假设z轴正方向指向下方。为了区分下行波和上行波,在给定水平慢度s1的情况下,求解s3的慢度关系式如下
s_3=\pm\frac1{\sqrt2}\sqrt{K_1\mp\mathcal{P}\sqrt{K_1^2-4K_2K_3}}
其中
\begin{aligned}K_1&=\rho\left(\frac{1}{p_{55}}+\frac{1}{p_{33}}\right)+\frac{1}{p_{55}}\left[\frac{p_{13}}{p_{33}}(p_{13}+2p_{55})-p_{11}\right]s_1^2\\K_2&=\frac{1}{p_{33}}(p_{11}s_1^2-\rho),\quad K_3=s_1^2-\frac{\rho}{p_{55}}.\end{aligned}
其符号正负对应的波
- (+,-)向下传播的qP波
- (+,+)向下传播的qSV波
- (-,-)向上传播的qP波
- (-,+)向上传播的qSV波
利用Eq.(1.81)和对应原理,可以从qP-qSV Kelvin-Christoffel方程中得到属于某一特定特征值的平面波特征向量(偏振)。我们获得
{{\bf{U}} = {U_0}\left( {\begin{array}{c}
\beta \\
\xi
\end{array}} \right)}
其中U0为平面波振幅
\beta = {\cal P}\sqrt {\frac{{{p_{55}}s_1^2 + {p_{33}}s_3^2 - \rho }}{{{p_{11}}s_1^2 + {p_{33}}s_3^2 + {p_{55}}(s_1^2 + s_3^2) - 2\rho }}}
\xi = \pm {\cal P}\sqrt {\frac{{{p_{11}}s_1^2 + {p_{55}}s_3^2 - \rho }}{{{p_{11}}s_1^2 + {p_{33}}s_3^2 + {p_{55}}(s_1^2 + s_3^2) - 2\rho }}}
+和-符号分别对应于qP和qSV波
上层用下标1表示,下层用下标2表示。P和S分别表示qP和qSV波。下标I、R和T分别表示入射波、反射波和透射波。利用对称性质定义反射波的偏振,给出了qP波从界面上方入射时的粒子速度
{{\bf{v}}_1} = {{\bf{v}}_{{{\bf{P}}_I}}} + {{\bf{v}}_{{{\bf{P}}_R}}} + {{\bf{v}}_{{{\bf{S}}_R}}}
{{\bf{v}}_2} = {{\bf{v}}_{{{\bf{P}}_T}}} + {{\bf{v}}_{{{\bf{S}}_T}}}
其中
\begin{array}{l}
{{\bf{V}}_{{{\bf{P}}_{\bf{I}}}}} = {\rm{i}}\omega ({\beta _{{{\rm{P}}_1}}},{\xi _{{{\rm{P}}_1}}})\exp [{\rm{i}}\omega (t - {s_1}x - {s_{3{{\rm{P}}_1}}}z)],\\
{{\bf{V}}_{{{\bf{P}}_{\bf{R}}}}} = {\rm{i}}\omega {R_{{\rm{PP}}}}({\beta _{{{\rm{P}}_1}}}, - {\xi _{{{\rm{P}}_1}}})\exp [{\rm{i}}\omega (t - {s_1}x + {s_{{\rm{3}}{{\rm{P}}_1}}}z)],\\
{{\bf{V}}_{{{\bf{S}}_{\bf{R}}}}} = {\rm{i}}\omega {R_{{\rm{PS}}}}({\beta _{{{\rm{S}}_1}}}, - {\xi _{{{\rm{S}}_1}}})\exp [{\rm{i}}\omega (t - {s_1}x + {s_{3{{\rm{S}}_1}}}z)],\\
{{\bf{V}}_{{{\bf{P}}_{\bf{T}}}}} = {\rm{i}}\omega {T_{{\rm{PP}}}}({\beta _{{{\rm{P}}_2}}},{\xi _{{{\rm{P}}_2}}})\exp [{\rm{i}}\omega (t - {s_1}x - {s_{{\rm{3}}{{\rm{P}}_2}}}z)],{\rm{ }}\\
{{\bf{V}}_{{{\bf{S}}_{\bf{T}}}}} = {\rm{i}}\omega {T_{{\rm{PS}}}}({\beta _{{{\rm{S}}_2}}},{\xi _{{{\rm{S}}_2}}})\exp [{\rm{i}}\omega (t - {s_1}x - {s_{{\rm{3}}{{\rm{S}}_2}}}z)]
\end{array}\tag{6.118}
边界条件要求v_1, v_2, \sigma_{33}, \sigma_{13}连续,速度公式代入应变应力关系, 边界条件产生如下关于反射和透射系数的矩阵方程:
\left.\left(\begin{array}{cccc}\beta_\mathrm{P_1}&\beta_\mathrm{S_1}&-\beta_\mathrm{P_2}&-\beta_\mathrm{S_2}\\\xi_\mathrm{P_1}&\xi_\mathrm{S_1}&\xi_\mathrm{P_2}&\xi_\mathrm{S_2}\\Z_\mathrm{P_1}&Z_\mathrm{S_1}&-Z_\mathrm{P_2}&-Z_\mathrm{S_2}\\W_\mathrm{P_1}&W_\mathrm{S_1}&W_\mathrm{P_2}&W_\mathrm{S_2}\end{array}\right.\right)\cdot\left(\begin{array}{c}R_\mathrm{PP}\\R_\mathrm{PS}\\T_\mathrm{PP}\\T_\mathrm{PS}\end{array}\right)=\left(\begin{array}{c}-\beta_\mathrm{P_1}\\\xi_\mathrm{P_1}\\-Z_\mathrm{P_1}\\W_\mathrm{P_1}\end{array}\right)
其中
X = \beta {p_{11}}{s_1} + \xi {p_{13}}{s_3}
Z = \beta {p_{13}}{s_1} + \xi {p_{33}}{s_3}
故计算反射系数和透射系数的步骤如下:
- 求解水平慢度s1, 其为独立参数。
- 计算s_{3P_1},s_{3S_1},s_{3P_2},s_{3S_2}, 因为都是向下传播的所以,s3的第一项符号为正,均匀波的s_{3P_1}可通过s_{3}=\cos\theta/v_{c}(\theta)求解
- 计算特征值\beta, \xi
- 计算Z, W
- 代入最终的计算公式求解反射系数与传输系数
非均匀波的系数
P315 非均匀波速度场V=(v1,v3)
\mathbf{v}=\mathrm{i}\omega\mathbf{U}\exp\left[\mathrm{i}\omega(t-s_{1}x-s_{3}z)\right]
慢度向量为\mathbf{s}_R=(\mathrm{Re}(s_1),\mathrm{Re}(s_3))
衰减向量为\alpha=-\omega(\mathrm{Im}(s_{1}),\mathrm{Im}(s_{3}))
对于非均匀波上述两个方向不相等
对于在海下产生的波
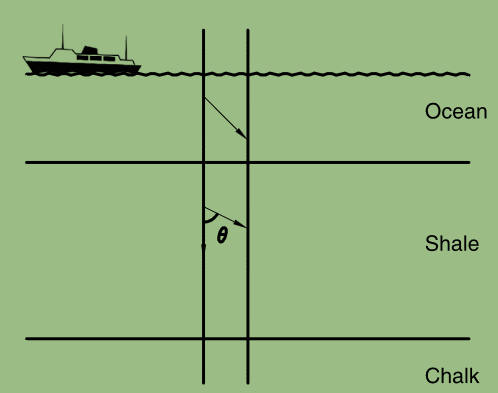
由于在水层中传播的波的衰减矢量为零,粘弹性Snell定律意味着透射波的衰减矢量垂直于海底。注意到非均匀性角等于传播角θ。
海底以下的复慢度分量是
s_1=s_R\sin\theta,\quad s_3=s_R\cos\theta-\frac{\mathrm{i}\alpha}{\omega}
对于给定角度θ, sR和α可由色散关系(4.168)计算。
该方法需要对两个四次多项式进行数值求解。计算量较大,可通过近似计算 P317, 这里不做介绍
分离固体和流体的界面
流体/固体界面在地震学和勘探地球物理学中具有重要意义,特别是在近海地震勘探中,海底是主要的反射事件之一。我们通过假设一个入射的均匀P波来考虑这个问题。
一组层的散射系数
在地震学中,一个平坦的分层系统可以很好地代表一个分层的地球。设一个水平复慢度为s1的平面波入射到正交介质的对称面上,如下图
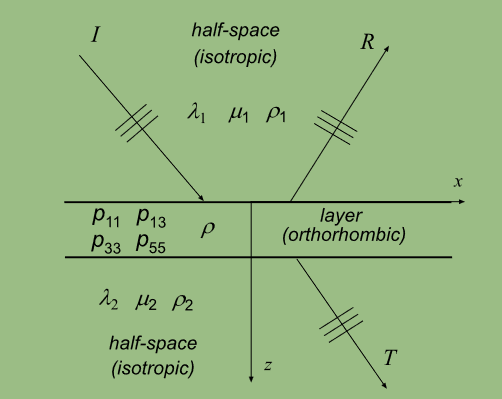
在层内,粒子速度场是上、下行准压缩波( P波)和准剪切波( S波)的叠加
\begin{array}{l}
{\bf{v}} = \left( {\begin{array}{c}
{{v_1}}\\
{{v_3}}
\end{array}} \right) = i\omega \left[ {U_{\rm{P}}^ - \left( {\begin{array}{c}
{{\beta _{\rm{P}}}}\\
{ - {\xi _{\rm{P}}}}
\end{array}} \right.} \right)\exp ({\rm{i}}\omega {s_{3P}}z) + U_{\rm{S}}^ - \left( {\begin{array}{c}
{{\beta _{\rm{S}}}}\\
{ - {\xi _{\rm{S}}}}
\end{array}} \right)\exp ({\rm{i}}\omega {s_{3S}}z)\\
\left. {\qquad \qquad \left. { + U_P^ + \left( {\begin{array}{c}
{{\beta _P}}\\
{{\xi _P}}
\end{array}} \right.} \right)\exp ( - {\rm{i}}\omega {s_{3P}}z) + U_S^ + \left( {\begin{array}{c}
{{\beta _S}}\\
{{\xi _S}}
\end{array}} \right)\exp ( - {\rm{i}}\omega {s_{3S}}z)} \right]\exp [{\rm{i}}\omega (t - {s_1}x)]
\end{array}\tag{6.153}
其中U−为上升波幅值,U +为下降波幅值,β和ξ为极化分量
法向的应力和应变关系为
\begin{aligned}&\mathrm{i}\omega\sigma_{33}=p_{13}\partial_1v_1+p_{33}\partial_3v_3,\\&\mathrm{i}\omega\sigma_{13}=p_{55}(\partial_3v_1+\partial_1v_3).\end{aligned}
故层内深度z处的粒子速度/应力阵列可以写成
\left.\mathbf{t}(z)=\left(\begin{array}{c}v_1\\v_3\\\sigma_{33}\\\sigma_{13}\end{array}\right.\right)=\mathbf{T}(z)\cdot\left(\begin{array}{c}U_\mathrm{P}^-\\U_\mathrm{S}^-\\U_\mathrm{P}^+\\U_\mathrm{S}^+\end{array}\right)
其中
{\bf{T}}(z) = {\rm{i}}\omega \left( {\begin{array}{r}
{{\beta _{\rm{P}}}}&{{\beta _{\rm{s}}}}&{{\beta _{\rm{P}}}}&{{\beta _{\rm{S}}}}\\
{ - {\xi _{\rm{P}}}}&{ - {\xi _{\rm{S}}}}&{{\xi _{\rm{P}}}}&{{\xi _{\rm{S}}}}\\
{ - {Z_{\rm{P}}}}&{ - {Z_{\rm{S}}}}&{ - {Z_{\rm{P}}}}&{ - {Z_{\rm{S}}}}\\
{{W_{\rm{P}}}}&{{W_{\rm{S}}}}&{ - {W_{\rm{P}}}}&{ - {W_{\rm{S}}}}
\end{array}} \right) \cdot \left(
{\begin{array}{c}
{\exp ({\rm{i}}\omega {s_{3P}}z)}&0&0&0\\
0&{\exp ({\rm{i}}\omega {s_{3S}}z)}&0&0\\
0&0&{\exp ( - {\rm{i}}\omega {s_{3P}}z)}&0\\
0&0&0&{\exp ( - {\rm{i}}\omega {s_{3S}}z)}
\end{array}} \right)
然后,z = 0和z = h处的场通过下面的方程联系起来:
\mathbf{t}(0)=\mathbf{B}\cdot\mathbf{t}(h),\quad\mathbf{B}=\mathbf{T}(0)\cdot\mathbf{T}^{-1}(h)\tag{6.157}
其中起到了边界条件的作用。注意到当h = 0时,B为单位矩阵
用下标1表示上半空间,用下标2表示下半空间.此外,下标I、R和T分别表示入射波、反射波和透射波。利用对称性质定义反射波的偏振,给出了P波从层上入射时的质点振速
\begin{aligned}\mathbf{v}_1&=\mathbf{v}_{\mathbf{P}_I}+\mathbf{v}_{\mathbf{P}_R}+\mathbf{v}_{\mathbf{S}_R},\\\mathbf{v}_2&=\mathbf{v}_{\mathbf{P}_T}+\mathbf{v}_{\mathbf{S}_T},\end{aligned}\tag{6.158}
反射透射速度可通过(6.118) 求得,其中极化分量由下式获得,
\left(\begin{array}{c}\beta_{\mathbf{P}}\\\xi_{\mathbf{P}}\end{array}\right)=\frac{1}{\sqrt{s_{1}^{2}+s_{3\mathbf{P}}^{2}}}\left(\begin{array}{c}s_{1}\\s_{3\mathbf{P}}\end{array}\right),\quad\left(\begin{array}{c}\beta_{\mathbf{S}}\\\xi_{\mathbf{S}}\end{array}\right)=\frac{1}{\sqrt{s_{1}^{2}+s_{3\mathbf{S}}^{2}}}\left(\begin{array}{c}s_{\mathbf{S}}\\-s_{1}\end{array}\right)
其中
s_{1}^{2}+s_{3\mathrm{P}_{i}}^{2}=\frac{\rho_{i}}{E_{i}}\equiv\frac{1}{v_{\mathrm{P}_{i}}^{2}},\quad s_{1}^{2}+s_{3\mathrm{S}_{i}}^{2}=\frac{\rho_{i}}{\mu_{i}}\equiv\frac{1}{v_{i}^{2}},\quad i=1,2,\tag{6.160}
根据(6.118),(6.158)1 z = 0处的质点速度/应力场可以表示为
\mathbf{t}(0)=\mathbf{A}_1\cdot\mathbf{r}+\mathbf{i}_\mathbf{P},\tag{6.163}
其中
\begin{aligned}\mathbf{r}&=(R_{\mathrm{PP}},R_{\mathrm{PS}},T_{\mathrm{PP}},T_{\mathrm{PS}})^\top,\\\mathbf{i}_{\mathrm{P}}&=\mathrm{i}\omega(\beta_{\mathrm{P_1}},\xi_{\mathrm{P_1}},-Z_{\mathrm{P_1}},-W_{\mathrm{P_1}})^\top,\end{aligned}
\mathbf{A}_1=\mathrm{i}\omega\left(\begin{array}{rrrr}\beta_{\mathbf{P}_1}&\beta_{\mathbf{S}_1}&0&0\\-\xi_{\mathbf{P}_1}&-\xi\text{s}_1&0&0\\-Z_{\mathbf{P}_1}&-Z_{\mathbf{S}_1}&0&0\\W_{\mathbf{P}_1}&W_{\mathbf{S}_1}&0&0\end{array}\right)
根据(6.118),(6.158)2 可得z = h处的粒子速度/应力场可以表示为
\mathbf{t}(h)=\mathbf{A}_{2}\cdot\mathbf{r}\tag{6.167}
其中
\mathbf{A}_2=\mathrm{i}\omega\left(\begin{array}{rrrr}0&0&\mathbf{\beta}_{\mathbf{P}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{P}_2}h)&\mathbf{\beta}_{\mathbf{S}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)\\0&0&\mathbf{\xi}_{\mathbf{P}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)&\mathbf{\xi}_{\mathbf{S}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)\\0&0&-Z_{\mathbf{P}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)&-Z_{\mathbf{S}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)\\0&0&-W_{\mathbf{P}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)&-W_{\mathbf{S}_2}\exp(-\mathrm{i}\omega s_{3\mathbf{S}_2}h)\end{array}\right)
根据公式(6.157),(6.163),(6.167) 得到反射系数和透射系数阵列r的矩阵方程
(\mathbf{A}_{1}-\mathbf{B}\cdot\mathbf{A}_{2})\cdot\mathbf{r}=-\mathbf{i}_{\mathbf{P}}\tag{6.169}
S波同理
无层时,h = 0, B为单位矩阵,得到6.2节的方程组。当上下半空间为同一介质时,可以得到pp波反射系数在正入射处的绝对值为
\mathrm{Rpp}(0)=\frac{2|R_0\sin(kh)|}{|R_0^2\exp(-\mathrm{i}kh)-\exp(\mathrm{i}kh)|}
考虑叠层地质系统,有N层,其刚度为pIJα,密度为ρα,每层厚度为hα,则总厚度为
h=\sum_{\alpha=1}^Nh_\alpha
通过在层与层之间的界面处匹配边界条件,很容易说明给出反射和透射系数的矩阵系统为
\left[\mathbf{A}_{1}-\left(\prod_{\alpha=1}^{N}\mathbf{B}_{\alpha}\right)\cdot\mathbf{A}_{2}\right]\cdot\mathbf{r}=-\mathbf{i}_{\mathbf{P}(\mathbf{S})}
其中
\mathbf{B}_{\alpha}=\mathbf{T}(0)\cdot\mathbf{T}^{-1}(\mathbf{h}_{\alpha}),\quad\alpha=1,\ldots,N
字母含义
角θ, δ和ψ表示传播,衰减和Umov-Poynting矢量(能量)方向
色散关系
F(s_1,s_3)=(p_{11}s_1^2+p_{55}s_3^2-\rho)(p_{33}s_3^2+p_{55}s_1^2-\rho)-(p_{13}+p_{55})^2s_1^2s_3^2=0\tag{4.168}

