线性代数¶

埋坑中........

矩阵乘法¶

一开始矩阵乘法是为了解决多元线性方程组的,通过不断行变换使该矩阵对应的系数矩阵为对角矩阵,增广矩阵的最后一列即为解向量, 可以参考马同学的从高斯消元法到矩阵乘法

仔细看看就会发现,如果一个矩阵,左乘一个矩阵,就是对原矩阵进行行变换,右乘一个矩阵就是对原矩阵进行列变换

更进一步看. 比如有GF=Z两个矩阵相乘得到Z, 可以看成Z由G的列为基构成的空间, 亦或是由F的行为基构成的空间, 但矩阵默认列向量为基, 所以就将看作有G的列为基构成的空间, 就是换基做了一种映射

如下定义了一种A(x)=y的映射, 相当于在A列空间中,坐标为 $[x_1,x_2]$ 和 $[x_3, x_4]$ 的矩阵在原始基空间的坐标是多少

$\left[ \begin{array}{l} 1 & 2 \\ 3 & 4 \end{array} \right] * \left[ \begin{array}{l} x_1 & x_2 \\ x_3 & x_4 \end{array} \right] = \left[ \begin{array}{l} x_1+2x_3 & x_2+2x_4 \\ 3x_1+4x_3 & 3x_2+4x_4 \end{array} \right] = \left[ \begin{array}{l} 1 & 0 \\ 0 & 1 \end{array} \right] * \left[ \begin{array}{l} y_1 & y_2 \\ y_3 & y_4 \end{array} \right]$

矩阵的特征值与特征向量¶

分解¶

空间¶

如何理解希尔伯特空间？ - 无尘粉笔的回答 - 知乎

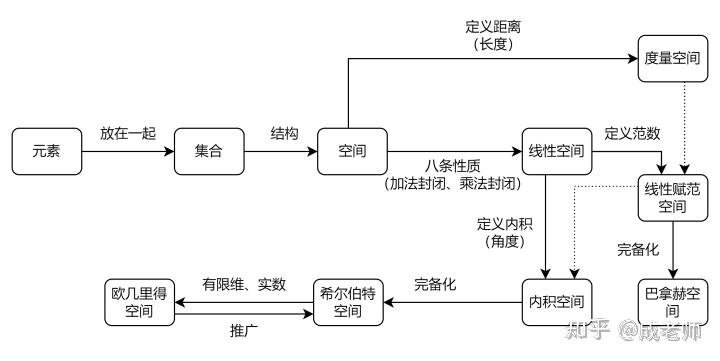
空间¶

把多个元素放在一起就构成了集合 $\{ x_1, x_2, \dots, x_n\}$ ，

度量空间(Metric space)¶

度量空间是具有距离这一个概念的集合,需满足

名称	内容
非负性	$d(x, y) \geq 0$
同一性	$d(x,y)=0\iff x=y$
对称性	$d(x,y)=d(y,x)$
三角不等式	$d(x,z)\leq d(x,y)+d(y,z)$

向量空间(线性空间)¶

向量空间是一群可缩放和相加的数学实域（如实数甚至是函数）所构成的特殊集合，其特殊之处在于缩放和相加后仍属于这个集合，给定一个域F和空间V

向量加法: 对于任意 $x, y \in V$ ， $x+y$ 也属于V
向量数乘: 对于任意 $c \in F, x \in V$ , $cx$ 也属于V

赋范向量空间(Normed vector space)¶

是具有“长度”概念的向量空间。是通常的欧几里得空间 $R^n$ 的推广。 $R^n$ 中的长度被更抽象的范数替代。“长度”概念的特征是：

名称	内容
非负性	$\\|\\|x\\|\\| \geq 0$
非退化性	$\\|\\|x\\|\\|=0\iff x=0$
齐次性	${\\|\\|\alpha x\\|\\|=\\|\alpha\\|\cdot\\|\\|x\\|\\|}$
三角不等式	$\\|\\|x+y\\|\\| \leq \\|\\|x\\|\\| +\\|\\|y\\|\\|$

一个把向量映射到非负实数的函数如果满足以上性质，就叫做一个半范数；如果只有零向量的函数值是零，那么叫做范数。拥有一个范数的向量空间叫做赋范向量空间，拥有半范数的叫做半赋范向量空间。

内积空间(Inner product space)¶

增添了内积运算的向量空间，它推广了原来欧几里德空间的点积，而从比较一般的角度看待向量的“夹角”、“长度”还有正交性。

内积空间有时也叫做准希尔伯特空间（pre-Hilbert space），因为由内积定义的距离完备化之后就会得到一个希尔伯特空间 👇

希尔伯特空间¶

巴纳赫空间¶

欧几里得空间¶

附录¶

柯西序列(Cauchy sequence)¶

在数学中，柯西序列、也称为基本列，是指一个元素随着序数的增加而愈发靠近的数列。柯西列一个重要性质是，在完备空间中，所有的柯西数列都有极限且极限在这空间里，这就让人们可以在不求出这个极限（如果存在）的情况下，利用柯西列的判别法则证明该数列的极限是存在的。