动态规划
动态规划¶
多维DP的入门经典!!
741摘樱桃 & 1462摘樱桃Ⅱ
灵神我的神!教你一步步思考 DP:从记忆化搜索到递推到空间优化!(Python/Java/C++/Go/JS/Rust)
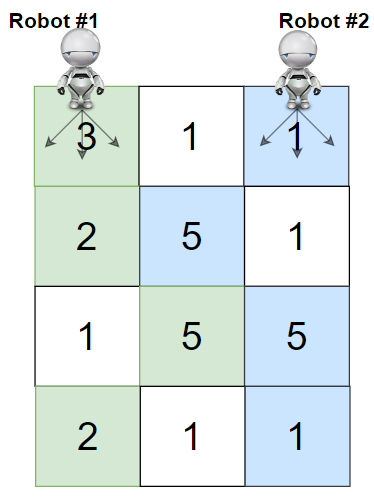
741摘樱桃
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
vector<vector<vector<int>>> f(n * 2 - 1, vector<vector<int>>(n, vector<int>(n, -1)));
f[0][0][0] = grid[0][0];
function<int(int, int, int)> dfs = [&](int t, int j, int k) -> int{
if (j < 0 || k < 0 || t < j || t < k || grid[t - j][j] < 0 || grid[t - k][k] < 0) {
return INT_MIN;
}
if(t==0)
{
return grid[0][0];
}
int& res = f[t][j][k]; // 注意这里是引用
if (res != -1) { // 之前计算过
return res;
}
return res = max({dfs(t - 1, j, k), dfs(t - 1, j, k - 1), dfs(t - 1, j - 1, k), dfs(t - 1, j - 1, k - 1)}) +
grid[t - j][j] + (k != j ? grid[t - k][k] : 0);//摘过的不再计算
};
return max(dfs(n * 2 - 2, n - 1, n - 1), 0);
}
};
1462摘樱桃Ⅱ
//dfs递归
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<vector<int>>> memo(n, vector<vector<int>>(m, vector<int>(m,-1)));
function<int(int, int, int)> dfs = [&](int i, int j, int k) -> int {
if(i<0||i>=n||j<0||j>=m||k<0||k>=m)
{
return 0;
}
int& res = memo[i][j][k]; // 注意这里是引用
if (res != -1) { // 之前计算过
return res;
}
for (int j2 = j - 1; j2 <= j + 1; j2++) {
for (int k2 = k - 1; k2 <= k + 1; k2++) {
res = max(res, dfs(i + 1, j2, k2));
}
}
res += grid[i][j] + (k != j ? grid[i][k] : 0);
return res;
};
return dfs(0,0,m-1);
}
};
//递推,将两个路径分为左右两个独立不交叉的路径,减小了dfs的循环次数
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<vector<int>>> f(n+1, vector<vector<int>>(m+2, vector<int>(m+2)));//从下到上,所以i要从n-1开始
for (int i = n - 1; i >= 0; i--)
{
for(int j = 0; j<min(m,i+1); j++)
{
for(int k = max(j+1, m-1-i); k<m; k++)
{
f[i][j + 1][k + 1] = max({
f[i + 1][j][k], f[i + 1][j][k + 1], f[i + 1][j][k + 2],
f[i + 1][j + 1][k], f[i + 1][j + 1][k + 1], f[i + 1][j + 1][k + 2],//将j-1, j, j+1更换成j,j+1,j+2这样就导致了数组长度加一(在最前方补了一个j-1)
f[i + 1][j + 2][k], f[i + 1][j + 2][k + 1], f[i + 1][j + 2][k + 2],
}) + grid[i][j] + grid[i][k];
}
}
}
return f[0][1][m];
}
};
//滚动数组代替了dp数组,减小空间开销
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<int>> pre(m+2, vector<int>(m+2));//滚动数组保存当前的和上一时刻的
vector<vector<int>> cur(m+2, vector<int>(m+2));
for (int i = n - 1; i >= 0; i--)
{
for(int j = 0; j<min(m,i+1); j++)
{
for(int k = max(j+1, m-1-i); k<m; k++)
{
cur[j + 1][k + 1] = max({
pre[j][k], pre[j][k + 1], pre[j][k + 2],
pre[j + 1][k], pre[j + 1][k + 1], pre[j + 1][k + 2],//将j-1, j, j+1更换成j,j+1,j+2这样就导致了数组长度加一(在最前方补了一个j-1)
pre[j + 2][k], pre[j + 2][k + 1], pre[j + 2][k + 2],
}) + grid[i][j] + grid[i][k];
}
}
swap(pre, cur);
}
return pre[1][m];
}
};
背包问题¶
01背包模板题: 494. 目标和
完全背包模板: 322. 零钱兑换
01背包为对于一个元素只能选或者不选,完全背包为对于一个元素可以重复选择或者不选
以下代码示例为完全背包的零钱兑换问题
枚举起点¶
选或不选¶
这两种方法已在回溯法->模板题 组合总和进行了总结,详细解释可在回溯法->模板题 组合总和浏览
//0-1 背包递归+记忆化搜索
int coinChange(vector<int>& coins, int amount) {
vector<vector<int>> memo(coins.size(), vector<int>(amount+1,-1));
//用前i种钱构成left的方案数,long long 为了防止+1使得int溢出
function<long long(int,int)> dfs = [&](int i, int left)->long long
{
if (left==0)
{
return 0;
}
if(i==coins.size()||left<0)
{
return INT_MAX;
}
int& res = memo[i][left];
if(res!=-1)
{
return res;
}
res = min(dfs(i,left-coins[i])+1,dfs(i+1, left));//选和不选
return res;
};
int res = dfs(0,amount);
return res==INT_MAX?-1:res;
}
递推动态规划¶
请注意,如果使用递归,边界条件判断是正常的,但是动态规划涉及到状态转移,可能会比dfs的记忆化数组要多一维,这一点有点绕
// 1:1递推
int coinChange(vector<int>& coins, int amount) {
//dp[i][j]表示使用前i种钱构成j的最小方案数
vector<vector<int>> dp(coins.size()+1, vector<int>(amount+1,INT_MAX/2));//防止+1溢出int
dp[0][0] = 0;//DP初值
for(int i = 0; i<coins.size();i++)
{
for(int j = 0; j<=amount;j++)
{
if(j<coins[i])//钱数小于单张金额,所以只能不选这个钱币
dp[i+1][j] = dp[i][j];
else//找出选与不选的最小值作为此时的方案数
dp[i+1][j] = min(dp[i+1][j-coins[i]]+1, dp[i][j]);
}
}
return dp[coins.size()][amount]<INT_MAX/2?dp[coins.size()][amount]:-1;
}
滚动数组空间优化¶
可以发现状态转移时dp[i+1]只和dp[i]有关,所以可以使用两个一维数组进行空间优化
int coinChange(vector<int>& coins, int amount) {
//由于dp[i][j]只与dp[i-1]有关,所以可以只定义2行,用取模的方式分别对其赋值
//也可以定义两个一维数组,pervious 和 current 代表当前和过去,每进行一次循环就swap一下
vector<vector<int>> dp(2, vector<int>(amount+1,INT_MAX/2));
dp[0][0] = 0;
for(int i = 0; i<coins.size();i++)
{
for(int j = 0; j<=amount;j++)
{
if(j<coins[i])
dp[(i+1)%2][j] = dp[i%2][j];
else
dp[(i+1)%2][j] = min(dp[(i+1)%2][j-coins[i]]+1, dp[i%2][j]);
}
}
return dp[coins.size()%2][amount]<INT_MAX/2?dp[coins.size()%2][amount]:-1;
}
一个数组空间优化¶
可以根据滚动数组的更新规律,在原数组上进行原地更新,这样只需要一个数组就行了,只需要bi
int coinChange(vector<int>& coins, int amount) {
vector<long long> dp(amount+1,INT_MAX);//dp[i]表示凑齐i需要的最少硬币数
dp[0] = 0;
for(int i = 1; i<=amount;i++)
{
for(int j = 0; j<coins.size();j++)//遍历coins找最小值即可
{
if(i>=coins[j])//可以尝试选一下
dp[i] = min(dp[i-coins[j]]+1,dp[i]);//看看选了之后是否变小了
// else
// dp[i] = dp[i]; //这里等价于不写
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
数位DP¶
数位 DP 通用模板,附题单(Python/Java/C++/Go)
字面意思就是说将数字的每一位做DP
拿例题举例(困难)
如果一个正整数每一个数位都是互不相同 的,我们称它是特殊整数 。给你一个 正整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
符合拿数字每一位做DP的场景, 结合DFS, 每次搜索从最高位开始直到符合条件的最低位,然后使res++
限制条件为
- 小于n
- 每位数都不同
故需要二维DP数组,第一维代表限制条件1,第二维代表限制条件2, 这里要保证每位数字不同使用了位运算, 定义10位二进制数, 代表0~9的存在情况
int dfs(int i, int mask, bool isLimit)
{
if(i==n)
return 1;
int max_bound = isLimit?s[i]-'0':9;
int res = 0;
for(int d = 0; d<=max_bound;d++)
{
if(mask>>d&1==0) // 前面没有用过这个数字才能继续dfs
res += dfs(i+1, mask|1<<d, isLimint && d==max_bound);
}
return res;
}
这样做绝对超时,因为有重复计算,这里就用到了记忆化搜索, python中可以通过装饰器@cache,内部会进行记忆化计算,但是c++需要自己定义记忆数组.
int dfs(int i, int mask, bool isLimit, bool isNum)
/*
i n的第几位
mask 代表已经选择过的数字,随着i更新
isLimit 如果为真说明前面的数都一样, 要保证小于n就要让之后的数字不能是0-9而应该是0-n[i]
isNum 当前状态前面是否填过数字,如果为真,则不能跳过
*/
{
if(i==m)
return isNum;//如果此时还是跳过的状态,则为0,
if(!isLimit && isNum && memo[i][mask]!=-1)
return memo[i][mask];
int res = 0;
if(!isNum)//当前跳过, 下一个可以继续跳过
res = dfs(i+1, mask, false, false); //跳过之后isLimit无限制
int max_limit = isLimit? s[i]-'0':9; //限制开始时一定是s的第一位
for(int j = 1-isNum; j<=max_limit; ++j)//如果isNum, 则可以从0开始填, 如果前面都跳过了, 则只能从1开始填
{
if((mask>>j&1)==0)//mask中没有这个数字,说明前面的所有数字不重复
{
res+=dfs(i+1,mask|(1<<j),isLimit&&j==max_limit,true);
// 状态转移方程
// mask要增加j这个值, 则对其进行或运算
// 如果上一阶段是isLimit且此时j==max_limit,则下一阶段也是isLimit
// 没有跳过所以isNum为true
}
}
//记忆状态
if(!isLimit&&isNum)//只有没有限制且没有跳过才保存当前值
memo[i][mask]=res;
return res;
}
区间DP¶
当前区间的状态由上一个区间的状态转移过来的一种DP, dp[i][j]表示区间[i,j]的值
模板解法
左区间递减,起点为n-1,终点为0
右区间递增,起点为i+1, 终点为n-1
在循环中更新数组元素
返回dp[0][n-1]即为区间[0,n-1]的值
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
dfs解法
int longestPalindromeSubseq(string s) {
int n = s.size();
//区间DP数组,memo[i][j]表示区间[i,j]的最大回文长度
vector<vector<int>> memo(n, vector<int>(n,-1));//由于状态转移时不需要额外的空间,所以长度为n
function<int(int,int)> dfs = [&](int l, int r)
{
if (l > r) return 0;//正好抵消成空串
if(l==r)
{
return 1;//正好留一个字母也是回文的,所以返回1
}
if(memo[l][r]!=-1)//记忆化数组
return memo[l][r];
if(s[l]==s[r])//如果首尾相等,说明可以构成回文,长度加2,区间长度减小2
{
memo[l][r]=dfs(l+1,r-1)+2;
}
else//删除头或者删除尾去进行递归
memo[l][r] = max(dfs(l+1,r),dfs(l,r-1));
return memo[l][r];
};
return dfs(0,n-1);
}
1:1翻译成递推,也就是正着实现递归,从最小的子问题开始循环
//灵神区间DP初探
int longestPalindromeSubseq(string s) {
int n = s.size();
//区间DP数组,dp[i][j]表示区间[i,j]的最大回文长度
vector<vector<int>> dp(n, vector<int>(n,0));//由于状态转移时不需要额外的空间,所以长度为n
for(int i = n-1; i>=0; i--)
{
dp[i][i] = 1;//[i,i]只有自己一个元素,所以构成回文串,长度为1,注意不能把dp数组全定义为1,原因如下
for(int j = i+1; j<n;j++)
{
if(s[i]==s[j])//首尾元素相同,可以构成回文
dp[i][j] = dp[i+1][j-1]+2;//不能把dp数组全定义为1原因在这里,如果遇到"aa"输出结果为3
else
dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][n-1];
}
滚动数组代替DP数组, 空间优化O(n^2)为O(n)
int longestPalindromeSubseq(string s) {
int n = s.size();
//滚动数组,根据状态转移方程发现更新dp[i]时仅仅需要dp[i+1]的值,所以可以定义一维数组保存上一索引的数
//per[j]表示上一个i索引到j的的最大回文长度,也就是per表示dp[i+1]
vector<int> per(n,0);
for(int i = n-1; i>=0; i--)
{
vector<int> cur(n,0);
cur[i] = 1;//[i,i]只有自己一个元素,所以构成回文串,长度为1
for(int j = i+1; j<n;j++)
{
if(s[i]==s[j])
cur[j] = per[j-1]+2;
else
cur[j] = max(per[j],cur[j-1]);
}
swap(cur,per);//cur变为per经行下一区间的计算
}
return per[n-1];//由于跳出循环时进行了swap,所以返回per
}
进阶题
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。 现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得
nums[i - 1] * nums[i] * nums[i + 1]枚硬币。 这里的i - 1和i + 1代表和i相邻的两个气球的序号。如果i - 1或i + 1超出了数组的边界,那么就当它是一个数字为 1 的气球。 求所能获得硬币的最大数量。
思路:
由于戳破气球后表示删除该气球,相邻关系要发生改变,所以这个要考虑进状态转移方程里,所以假设在开区间(i,j)中最后一次戳破k气球,此时k气球相邻气球为i,j,这就满足了相邻关系的改变
随想:
我自己当时想的状态转移是val[k-1]*val[k]*val[k+1],但后来发现这表示的是第一次戳破的是第k个气球,这样的话无法表示对第k个气球进行删除的操作,而val[i] * val[k] * val[j]表示的是最后一次戳破k气球,并删除了开区间(l,k)和(k,r)的元素的操作
细节:
- dp数组的大小为
[n+2, n+2]是因为状态转移时需要超出区间两个元素,分数分别为1,所以可以重新构建一个n+2长度的val数组 - 由于区间DP时还有循环
(i,j)中的元素进行k的选择,所以无法使用滚动数组优化
//官解
//区间DP进阶,之前看过一遍这个题,以为能秒,结果发现考虑的还是太浅了
int maxCoins(vector<int>& nums) {
int n = nums.size();
vector<int> val(n + 2);
val[0] = val[n + 1] = 1;
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
vector<vector<int>> dp(n+2, vector<int>(n+2));//DP数组表示开区间(i,j)戳破的最大分数
for(int i = n-1; i>=0; i--)//左区间递减
{
for(int j = i+2; j<=n+1; j++)//右区间递增,由于是开区间,所以需要i+2为起点
{
for(int k = i+1; k<j; k++)//这里的k表示在(l, r)区间内最后一个被戳破的气球,那么此时与它相邻的两个气球为val[l]和val[r]
{
dp[i][j] = max(dp[i][k]+val[i]*val[k]*val[j]+dp[k][j],dp[i][j]);//状态转移
}
}
}
return dp[0][n+1];//注意返回值,应该是i和j的终点
}
官解转dfs
//官解转dfs
int maxCoins(vector<int>& nums) {
int n = nums.size();
vector<int> val(n + 2);
val[0] = val[n + 1] = 1;
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
vector<vector<int>> dp(n+2, vector<int>(n+2,-1));//DP数组表示开区间(i,j)戳破的最大分数
function<int(int,int)> dfs = [&](int l, int r)
{
if(l+1==r)//开区间结束的条件就是l+1==r,此时区间(l,l+1)中无元素
{
return 0;
}
if(dp[l][r]!=-1)
{
return dp[l][r];
}
int& res = dp[l][r];
for(int k = l+1; k<r; k++)
{
res = max(res, dfs(l,k)+dfs(k,r)+val[l]*val[r]*val[k]);
}
return res;
};
return dfs(0,n+1);//注意返回值,应该是i和j的终点
}
状态机DP¶
顾名思义,就是DP转移时要根据不同状态进行不同的状态转移方程, 拿周赛的题举例子
题目解读:将区间划分为若干子区间,子区间中的数符号为正负交替(第一个必须为正), 要使这样做之后的区间和最大
问题转化: 最大值问题可以通过DP求解, 关键就是dp数组的定义和状态转移方程的建立,假定dp[i]表示到[0,i]区间的最大成本,那么就要找其状态转移方程,[0,i+1]的最大成本有两种情况,一种是从i之后处分割cost[i+1]不变号,加上dp[i], 一种就是i+1要变号, 就是dp[i-1]-cost[i+1], 这也是我周赛时的思路,代码实现一下
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
vector<long long> dp(n+1);//因为状态转移涉及到三个相邻元素, dp[n+1]表示结尾是n-1元素的最大值
dp[0] = 0;
dp[1] = nums[0];//要固定第一个数必须是正数
for(int i = 1; i<n; i++)
{
dp[i+1] = max(dp[i]+nums[i],dp[i-1]+nums[i-1]-nums[i]);
}
return dp.back();
}
ac了,但是当时没有想清楚其中的道理,仅仅是凭直觉写的转移方程,接下来我们就告诉你为什么可行,并且给出一套通用的状态机DP模板
之前的思路不好解释的原因就在于转移方程,我们尝试修改让他逻辑更清晰一些,定义dp[i][j]为区间[0,i]中且在这个点分割状态为j的最大值(定义j=0时,没有变号,j=1时变号了),这样状态转移方程就可以根据j的情况而进行更改,用递归实现一下
递归¶
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
vector<array<long long, 2>> memo(n, {LLONG_MIN,LLONG_MIN});//记忆化数组
auto dfs = [&](auto&& dfs, int i, int j)->long long
{
if(i==n)
return 0;
auto& res = memo[i][j];
if(res!=LLONG_MIN)
return res;
if(j==1)//i发生了变号
{
res = dfs(dfs, i+1, 0)+nums[i];//下一个元素必须不变号
}
else//i没有发生变号,之后的元素
{
res = i==0?dfs(dfs, i+1, 0)+nums[i]:max(dfs(dfs, i+1, 1)-nums[i], dfs(dfs, i+1, 0)+nums[i]);//i==0时首元素必须不变号
}
return res;
};
return dfs(dfs, 0, 0);
}
另一种写法 memo[i][j]表示区间[0,i]且i变号状态为j(还未发生)的最大成本,这两种写法理解一种就行
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
vector<array<long long, 2>> memo(n, {LLONG_MIN,LLONG_MIN});//记忆化数组
auto dfs = [&](auto&& dfs, int i, int j)->long long
{
if(i==n)
return 0;
auto& res = memo[i][j];
if(res!=LLONG_MIN)
return res;
if(j==1)//元素i要变号
{
res = dfs(dfs, i+1, 0)-nums[i];
}
else//元素i不变号
{
res = max(dfs(dfs, i+1, 1)+nums[i], dfs(dfs, i+1, 0)+nums[i]);//i==0时首元素必须不变号
}
return res;
};
return dfs(dfs, 0, 0);
}
递推写法¶
正序转移方程就是,当前时刻怎么做能转移到下一时刻
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
vector<array<long long, 2>> dp(n+1, {0,0});
dp[0][0] = nums[0];
for(int i = 0; i<n; i++)
{
dp[i+1][0] = i==0?nums[0]:max(dp[i][0]+nums[i],dp[i][1]-nums[i]);
dp[i+1][1] = dp[i][0]+nums[i];
}
return max(dp[n][1],dp[n][0]);
}
倒序转移方程就是,当前时刻的状态需要前一时刻怎么转移
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
vector<array<long long, 2>> dp(n+1, {0,0});//dp[i][j]表示以i为起点且i状态为j的最大值
for(int i = n-1; i>=0; i--)
{
dp[i][0] = max(dp[i+1][0]+nums[i],dp[i+1][1]+nums[i]);//当前状态不变号
dp[i][1] = dp[i+1][0]-nums[i];//当前状态要变号
}
return dp[0][0];
}
空间优化¶
由于dp[i]只与dp[i+1]有关,所以可以利用循环记住之前数,然后定义两个状态的遍历就好
long long maximumTotalCost(vector<int>& nums) {
int n = nums.size();
long long j0 = 0; j1=0;//表示两种状态的最大值
long long temp;
for(int i = n-1; i>=0; i--)
{
temp = j0;
j0 = max(j0,j1)+nums[i];
j1 = temp-nums[i];
}
return j0;
}
股票
正着递归时:没有股票时,可以选择买入进而到下一个时刻, 所以是-price[i], dp[i][j]表示[0,i]区间的最大利润
倒着递归时:没有股票时,可以由前一个时刻卖掉了进而到了这个时刻, 所以是+price[i], dp[i][j]表示[i,n-1]区间的最大利润
对于含冷冻期的题目来说正着递归不适用,因为当前时刻如果买的话取决于前两个时刻的值,倒着递归到i时,i-1, i-2都被计算过,直接取就可以,但是倒着递归时,无法得到之前(i-2)的状态, 因为那个状态还没有被计算到
如果加入限制次数K,就在dp数组加一维表示次数,dp[i][j][t]表示[0,i]进行j次交易的最大利润, 初始化很重要, 全部为INT_MIN, 其中dp[0][j][0]为0
题单¶
状态压缩¶
朴素解法¶
int countArrangement(int n) {
vector<vector<int>> memo(n+1, vector<int>(1<<n, -1));//i个数字且从集合中拿数状态为j的合法排列数量
auto dfs = [&](auto&& dfs, int i, int s)->int
{
if(i==n+1)
return 1;
int& res = memo[i][s];
if(res!=-1)
return res;
res = 0;
//j表示perm[i],取值为1-n
for(int j = 0; j<n; j++)
{
if((s>>j&1)==0&&(i%(j+1)==0||(j+1)%i==0))//j+1这个数可以放到i这个位置
{
res += dfs(dfs, i+1, s^(1<<j));
}
}
return res;
};
return dfs(dfs, 1, 0);//由于i从1开始
}
空间优化¶
由于排列中的数字个数可以通过状态s中1的个数确定,所以可以省略第一个维度, 通过gcc内置函数__builtin_popcount()来统计1的个数来获得i
正着递归 入口dfs(0)¶
int countArrangement(int n) {
vector<int> memo(1<<n, -1);//集合中拿数状态为i的合法排列数量
auto dfs = [&](auto&& dfs, int s)->int
{
if(s==(1<<n)-1)
return 1;
int& res = memo[s];
if(res!=-1)
return res;
int i = __builtin_popcount(s)+1;//i从1开始
res = 0;
//j表示perm[i],取值范围为[1,n]
for(int j = 0; j<n; j++)
{
if((s>>j&1)==0&&(i%(j+1)==0||(j+1)%i==0))//j+1这个数可以放到i这个位置
{
res += dfs(dfs, s^(1<<j));
}
}
return res;
};
return dfs(dfs, 0);
}
倒着递归 入口dfs(n)¶
int countArrangement(int n) {
vector<int> memo((1<<n), -1);//集合中拿数状态为i的合法排列数量
auto dfs = [&](auto&& dfs, int i)->int
{
if(i==0)
return 1;
int& res = memo[i];
if(res!=-1)
return res;
int k = __builtin_popcount(i);
res = 0;
for(int j = 0; j<n; j++)
{
if(i>>j&1&&(k%(j+1)==0||(j+1)%k==0))//j这个数可以放到k这个位置
{
res += dfs(dfs, i^(1<<j));
}
}
return res;
};
return dfs(dfs, (1<<n)-1);
}